基本块、流图、循环

基本块

基本块指程序中一个顺序执行的语句序列，只有一个入口和出口语句，除入口语句外不可以带标号，除出口语句外不可以跳出

入口语句可能是：

  • 程序的第一个语句
  • 带标号语句：可以作为条件跳转或无条件跳转语句的目标语句
  • 条件转移语句的后一条语句

注：基本块是在 函数 的层次内讨论的，进而函数调用在基本块的分析中视为顺序执行的语句，函数返回在基本块的分析中视为停语句；跨函数讨论基本块、流图等没有意义

流图

流图或控制流图，简称CFG，是用有向图表示基本块之间可能的控制流的数据结构

流图的结点集是基本块集，第一个结点是程序的起始基本块；基本块ii到基本块jj存在有向边当且仅当基本块ii可以转移到基本块jj

循环

首先定义支配结点：如果从流图的首结点出发，要到达nn必须先经过mm，则称mm是nn的支配结点，记为m DOM nm\ {\rm DOM}\ n

结点nn的所有支配结点的集合定义为其支配结点集，记为D(n)D(n)

接下来定义自然循环：如果d DOM nd\ {\rm DOM}\ n，但存在有向边n→dn\to d，则n→dn\to d称为一条回边（注意到它和支配的顺序相反，由被支配点指向支配点）

每条回边对应了一个自然循环：自然循环是一个结点集，包含回边的首末结点，和不经过dd就可以到达nn的所有节点的集合

  • 因此，自然循环中的点不一定总是构成一个圈，也可能构成一个多环的桥环结构
  • 所谓“不经过dd就可以到达nn”，实际上根据支配结点的定义就可以知道，这样的点不会包含首节点

数据流分析

数据流分析通过建立和求解数据流方程，来获得对代码生成和代码优化工作有意义的数据流信息，并将这些信息分配到流图中的语句单元

典型的数据流方程举例：

out[S]=gen[S]∪(in[S]−kill[S]){\rm out}[S]={\rm gen}[S]\cup({\rm in}[S] - {\rm kill}[S])

即：离开某个基本块SS的数据流信息由两部分组成：在SS内产生的信息，和进入SS且未被杀死的信息

到达-定值数据流分析

到达-定值数据流分析是在流图中以正向进行的数据流分析，其数据流分析的基本单元是定值点，表示一条具有赋值性质的语句位置

其基本方程为：

out[S]=gen[S]∪(in[S]−kill[S]){\rm out}[S]={\rm gen}[S]\cup({\rm in}[S] - {\rm kill}[S])

in[B]=⋃b∈P[B]out[b]{\rm in}[B]=\bigcup_{b\in P[B]}{\rm out}[b]

其中P[B]P[B]为BB的前驱结点集，gen[B]{\rm gen}[B]为BB中所有得到定值且定值持续到出口还有效的定制点集合，kill[S]{\rm kill}[S]表示在BB内发生重新定值而被杀死的定值点集合

求解数据流方程只需要对所有基本块反复迭代上述方程直到不发生改变即可

  • 可以先完成gen\rm gen和kill\rm kill的计算，再迭代计算in\rm in和out\rm out

活跃变量数据流分析

活跃变量数据流分析在流图中以逆向进行，其数据流分析的基本单元是变量，一个变量在某个程序点是活跃的表示它在此点的值仍然需要保持（在此点之后可能被引用）

活跃变量的数据流方程：

LiveIn[B]=LiveUse[B]∪(LiveOut[B]−Def[B]){\rm LiveIn}[B]={\rm LiveUse}[B]\cup({\rm LiveOut}[B]-{\rm Def}[B])

LiveOut[B]=⋃s∈S[B]LiveIn[s]{\rm LiveOut}[B]=\bigcup_{s\in S[B]}{\rm LiveIn}[s]

其中S[B]S[B]表示BB的后继结点集，其他含义在字面中即可以理解：

  • LiveUse\rm LiveUse：在块内存在定值前引用
  • Def\rm Def：在块内被定值

求解算法仍然是迭代至无改变，可以先计算LiveUse\rm LiveUse和Def\rm Def

到达定值和活跃变量两种分析模式的差异：

  • 前者是向前流，即数据流和控制流方向一致；后者是向后流，即方向相反
  • 前者不考虑变量的引用而只考虑定值；后者考虑引用，可以忽略无意义的定值

UD链和DU链

一个变量的某个引用点的UD(引用-定值)链表示可能影响这次引用的所有定值点组成的全体，即UD是引用点到定值点集合的映射

  • 如果在基本块内，引用点uu前存在定值点，则UD链只包括最近的定值点
  • 如果在基本块内引用点前没有定值点，则In[B]{\rm In}[B]中的所有对此变量的定值点都在UD链中

一个变量的某个定值点的DU链类似，表达此定值点可以影响到的引用点组成的全体，计算方法略

待用信息和活跃信息

待用信息和活跃信息是在基本块内起效的数据流信息，具体地：

  • 待用信息表示某定值点在基本块范围内最近的引用点
  • 活跃信息表示以语句为单位的活跃变量信息

基本块的DAG表示

DAG：有向无环图（Directed Acyclic Graph）

基本块的DAG是一个表达式图：

  • 叶节点表示名字的初值，用变量名字或常数标记（例如11或x0x_0，x0x_0表示变量xx在进入此基本块前的初始值）
  • 内部节点用运算符号标记
  • 每个节点都有一个附加的变量名字表

DAG表示的构造

设函数node(name)返回关联于name的最近的结点

首先置DAG为空，对每一条语句（仅考虑x:=y op z; x:=op y; x:=y三种）依次进行：

  • 若node(y)或node(z)无定义，为其创建叶节点
  • 对于二元运算语句
    • 若node(y)和node(z)都是常数，则直接计算，得到的新常数为p，如果node(p)无定义则构造，有定义则直接关联（可以静态计算已知量并合并相同的已知量）
    • 如果node(y)和node(z)至少一个不是常数，则检查是否存在已经计算好的node(y) op node(z)，如果有，直接关联，如果没有，再新建（可以合并相同的计算值）
  • 一元运算语句和直接赋值语句类似
    • 直接赋值语句在完成节点构造后还需要将原来的node(x)的附加标识符表中将x删除（可以删除无用赋值）

总的来说，基本块的DAG构造可以用来进行一定的静态优化：

  • 合并已知量
  • 删除多余运算
  • 删除无用赋值
  • 复写传播

目标代码生成

代码生成主要需要考虑的问题：

  • 指令选择
  • 寄存器分配
  • 指令调度
    • 根据目标机的特点安排计算次序

表达式树求值的寄存器优化

表达式树求值可以使用Ershov数和Sethi-Ullman算法来优化至最少的寄存器数目

一棵表达式树的Ershov数定义为完成此树求值所需要的寄存器数目的最小值

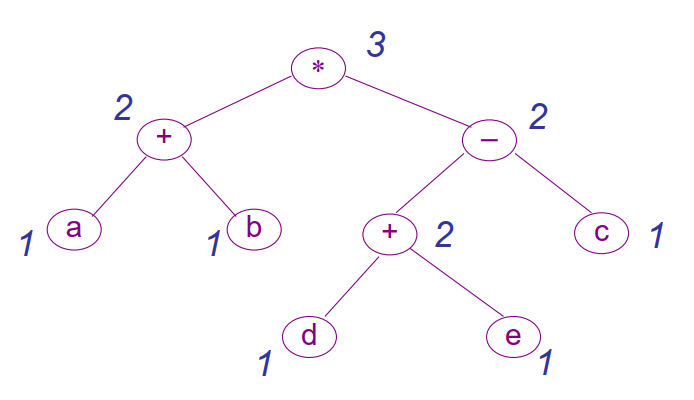
image-20250103184734729

上图表示了表达式树的Ershov数。注意这里没有进行相同子表达式的合并，进行了合并的表达式树会变成上一节中的DAG

Ershov数的计算规则如下：

  • 叶节点为对变量的引用或常数，叶节点定为11，常数定为00（有的实现也按11处理，此时会先把常数装入寄存器；这可以灵活地改变）
  • 对于内部节点，如果是一元运算符，则其Ershov数等于子节点的Ershov数
  • 如果是二元运算符，设子节点的Ershov数分别为xx和yy，则运算符节点的Ershov数由以下函数确定：
    • f(x,y)={max⁡(x,y),x≠yx+1,x=yf(x,y)=\begin{cases}\max(x,y),&x\neq y\\x+1,&x=y\end{cases}

使用Sethi-Ullman算法可以构造出符合Ershov数的寄存器使用最少的求值算法，其思想非常简单，只需要对二元运算符的子节点计算顺序进行调整：

  • 对于两个子节点Ershov数相等的情况，可以任意选择计算顺序
  • 对于两个子节点Ershov数不等的情况（两个数设为xx和yy，x>yx>y）：
    • 如果先计算xx，那么需要在保留一个寄存器存放xx子树的结果的同时计算yy，需要max⁡(x,y+1)=x\max(x, y+1)=x哥寄存器
    • 如果先计算yy，那么同理，需要max⁡(x+1,y)=x+1\max(x+1,y)=x+1个寄存器
    • 因此，总是先计算Ershov数大的子树

图着色寄存器分配算法

核心目的：spill到内存的寄存器数目最少

构造寄存器相干图：

  • 对每个伪寄存器构造一个结点
  • 如果在某个程序点处，两个结点同时活跃，即相干，则在两个结点间连边
  • 对相干图进行k-着色，其中k为物理寄存器数量；使任何相邻结点具有不同的颜色

能否k-着色是NP-完全问题，可以使用一个启发式着色算法：

  • 重复删去图中所有度数小于k

代码优化技术

按优化范围分类：

  • 窥孔优化：范围为几条指令
  • 局部优化：基本块内
  • 全局优化：流图范围内（过程内）
  • 过程间优化

按优化对象分类：

  • 目标代码优化
  • 中间代码优化
  • 源级优化（优化源代码）

窥孔优化

  • 合并已知量
    • r2:=3*2→r2:=6
  • 常量传播
    • r2:=4; r3:=r1+r2→r2:=4; r3:=r1+4
  • 代数化简
    • 删去x:=x+0、y:=y*1等
  • 控制流优化
    • goto L1; ... ; L1: goto L2→goto L2; ... ; L1: goto L2
  • 死代码删除
    • debug:=false; if(debug) ...→debug:=false
  • 强度削弱
    • x:=2.0*f→x:=f+f
  • 使用目标机惯用指令
    • +1使用+1指令
    • *2使用左移指令

基本块内优化

体现在DAG构造过程中

全局优化

  • 全局公共表达式删除
  • 全局死代码删除

循环优化

  • 代码外提
    • while (i<limit/2) {}→t:=limit/2; while (i<t) {}
    • 循环不变量的计算代码x:=y+z可以外提的条件：
      • 是循环不变量（y和z定值都在循环外）
      • 是循环所有出口的支配结点，或x在出循环后不再活跃（不会产生不该产生的副作用）
      • 循环其他地方不会给x定值
      • 循环中x所有引用点都可以由这个定值达到
  • 归纳变量（在循环每个迭代中自增/自减等的变量）优化