滤波器的类别

滤波器：一个作用在频域上的窗函数

一般讨论频域范围为[−π,π][-\pi, \pi]，然而滤波器必须为偶函数（否则统一频率的正负分量被滤过的情况不同），于是一般只考虑[0,π][0,\pi]上的情况即可

  • 高通滤波器(HP)
  • 低通滤波器(LP)
  • 带通滤波器(BP)
  • 带阻滤波器(BS)
  • 全通滤波器(AP)

滤波器的参数（设其函数形式为w(ω)w(\omega)，对低通滤波器讨论）

  • dpd_p：通带容限，表示max⁡ωw(ω)−1\max\limits_{\omega} w(\omega)-1，ω: ∣w(ω)−1∣≤dp\omega:\ |w(\omega)-1|\leq d_p组成的区间为通带，通带的边缘频率为ωp\omega_p
  • dsd_s：阻带容限，表示滤波器旁瓣的最大值，ω: w(ω)≤ds\omega:\ w(\omega)\leq d_s组成的区间为阻带，阻带的边缘频率为ωs\omega_s
  • 理想滤波器截止频率：定义为ωc=w−1(1/2)\omega_c=w^{-1}(1/2)
  • ωp\omega_p和ωs\omega_s之间为过渡带，合理的滤波器应满足ωc\omega_c位于过渡带中点
  • 实际滤波器截止频率：定义为w−1(1/2)w^{-1}(1/\sqrt{2})

即：对于低通滤波器，ωd<ωc<ωs\omega_d < \omega_c < \omega_s，对于高通滤波器则是ωs<ωc<ωd\omega_s<\omega_c<\omega_d

系统

系统是具有特定功能的整体，对信号进行某些特定操作

系统的分类

线性系统：满足叠加性和齐次性的系统

时不变系统：系统的输出与时间无关，任何时刻给出同一输入，系统的输出都是相同的；反之为时变系统

线性时不变系统简称LTI系统

因果系统：系统输出只与当前及以前时间的输入有关，与以后时间的输入无关；所有实际系统都是因果系统

稳定系统：输入有界时，输出也有界，即BIBO原则

系统的描述方法

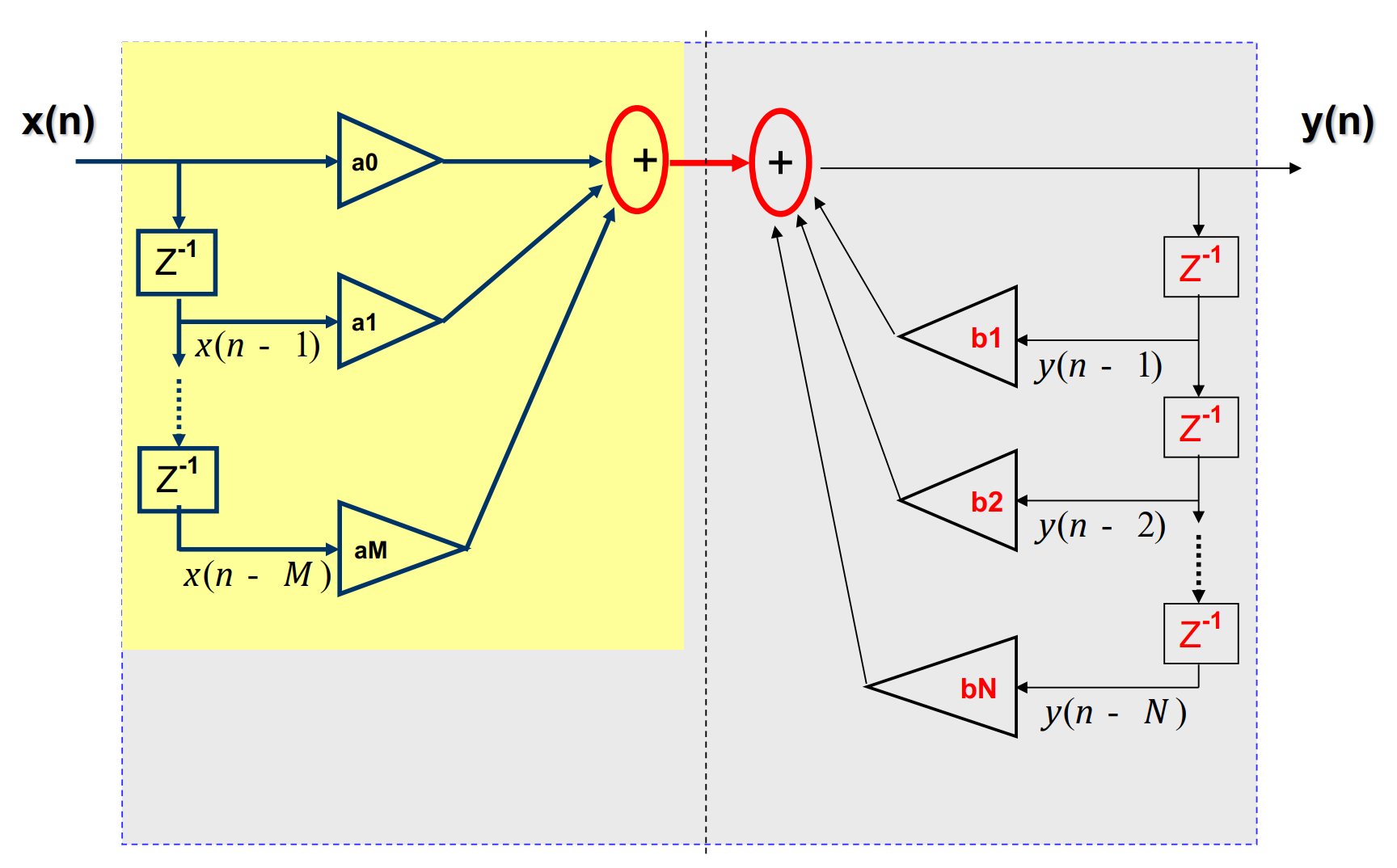
差分方程

y(n)=1b0[a0x(n)+a1x(n−1)−b1y(n−1)]y(n)=\frac{1}{b_0}[a_0x(n)+a_1x(n-1)-b_1y(n-1)]

更一般地

∑k=0Nbky(n−k)=∑r=0Marx(n−r)\sum\limits_{k=0}^{N}b_ky(n-k)=\sum\limits_{r=0}^{M}a_rx(n-r)

上述公式中的字母使用是规范，不要改变

NN为滤波器涉及的过去输出的个数，也被称为滤波器的阶数

一个速记方法：X-arm, Bynk

流图

见PPT，懒得写了:(

系统的激励和响应

从系统的角度，输入被称为激励，输出被称为响应

零输入响应：系统在没有任何激励信号作用时产生的信号输出

零状态响应：系统内部没有承载信息的能力，给系统激励信号后产生的输出

滤波器的脉冲响应或冲激响应，指的是滤波器的输入是脉冲信号时产生的响应

例如单位冲激

δ(n)={1,n=00,n≠0\delta(n)=\begin{cases}1,&n=0\\0,&n\neq 0\end{cases}

例：求下列滤波器脉冲响应的前6个采样值

y(n)=14[x(n)+x(n−1)+x(n−2)+x(n−3)]y(n)=\frac{1}{4}[x(n)+x(n-1)+x(n-2)+x(n-3)]

解：

h(n)=14[δ(n)+δ(n−1)+δ(n−2)+δ(n−3)]h(n)=\frac{1}{4}[\delta(n)+\delta(n-1)+\delta(n-2)+\delta(n-3)]

则

[h(0), h(1), ⋯ , h(5)]=[14,14,14,14,0,0][h(0),\ h(1),\ \cdots,\ h(5)]=[\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4},0,0]

有限脉冲响应(FIR)滤波器：有限输入后输出总会归零

y(n)=∑r=0Marx(n−r)y(n)=\sum\limits_{r=0}^{M}a_rx(n-r)

无限脉冲响应(IIR)滤波器：一般意义下的滤波器，经过有限输入后输出不一定归零

对于FIR滤波器，很多时候使用级联表达会比直接写出差分方程更加稳定

对于IIR滤波器，流图需要增加右侧的反向边，然后变换如下：

image-20241203162117666

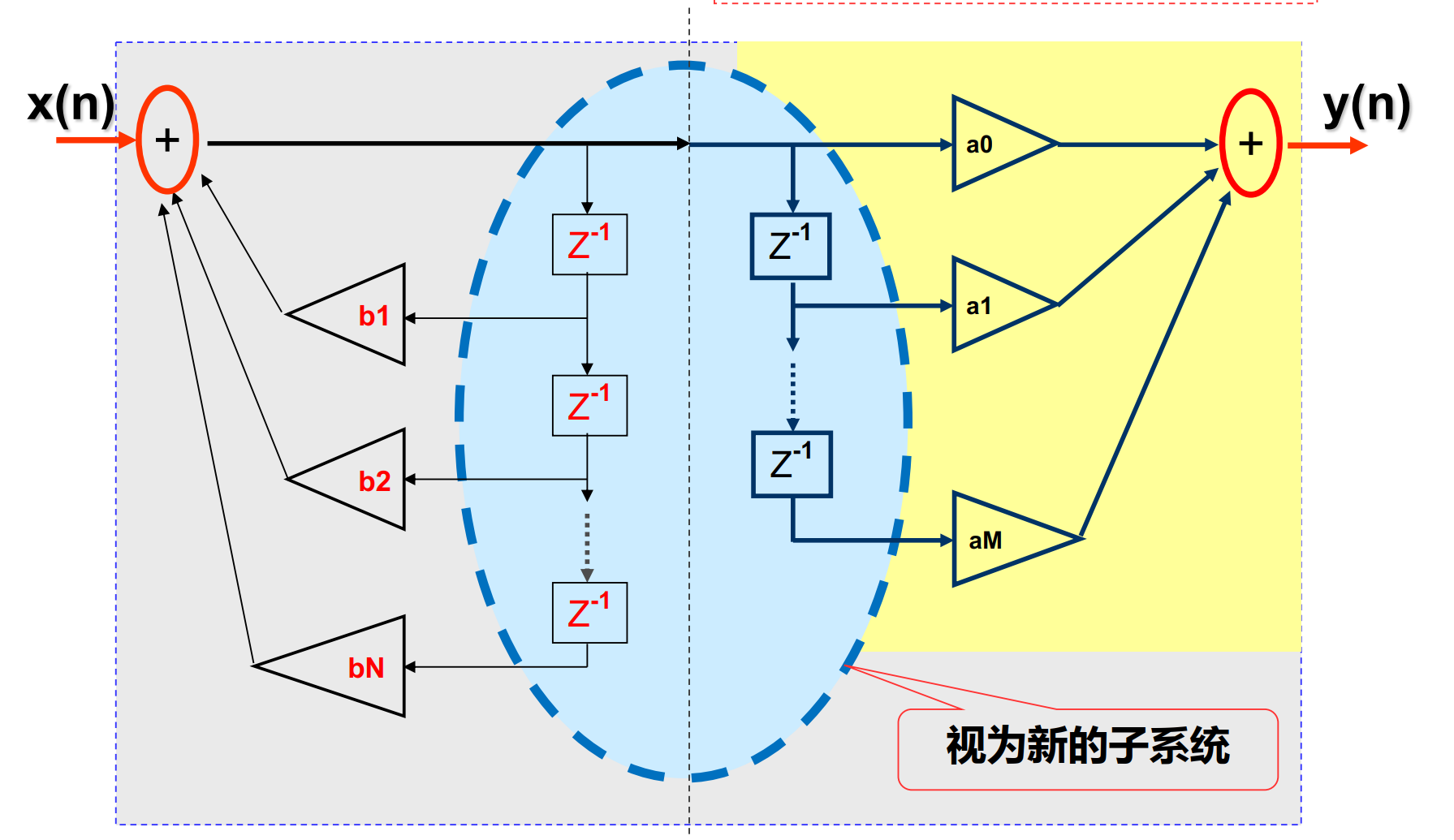
image-20241203162142200

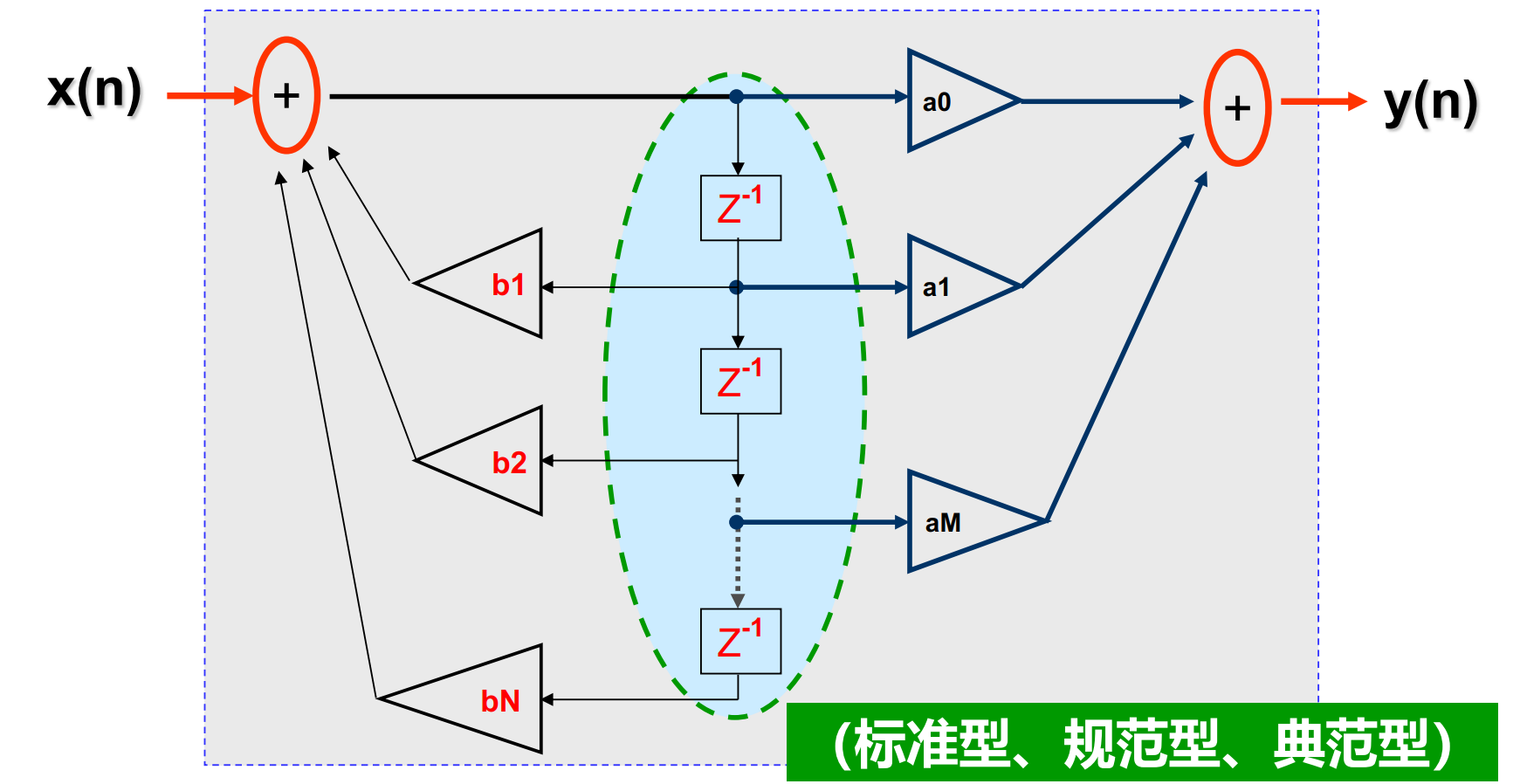
image-20241203162200288

证明：上面的变换前后的流图是等效的

设变换后第一个求和后的信号为z(n)z(n)，则

z(n)=x(n)+b1z(n−1)+⋯+bNz(n−N)=x(n)+∑k=1Nbkz(n−k)z(n)=x(n)+b_1z(n-1)+\cdots+b_Nz(n-N)=x(n)+\sum\limits_{k=1}^{N}b_kz(n-k)

而右侧为

y(n)=a0z(n)+⋯+aMz(n−M)=∑r=0Marz(n−r)y(n)=a_0z(n)+\cdots+a_Mz(n-M)=\sum\limits_{r=0}^{M}a_rz(n-r)

于是

y(n)=∑r=0Mar(x(n−r)+∑k=1Nbkz(n−r−k))y(n)=\sum\limits_{r=0}^{M}a_r(x(n-r)+\sum\limits_{k=1}^{N}b_kz(n-r-k))

=∑r=0Marx(n−r)+∑r=0M(ar∑k=1Nbkz(n−r−k))=\sum\limits_{r=0}^{M}a_rx(n-r)+\sum\limits_{r=0}^{M}\left(a_r\sum\limits_{k=1}^{N}b_kz(n-r-k)\right)

=∑r=0Marx(n−r)+∑k=1N(bk∑r=0Marz(n−r−k))=\sum\limits_{r=0}^{M}a_rx(n-r)+\sum\limits_{k=1}^{N}\left(b_k\sum\limits_{r=0}^{M}a_rz(n-r-k)\right)

=∑r=0Marx(n−r)+∑k=1Nbky(n−k)=\sum\limits_{r=0}^Ma_rx(n-r)+\sum\limits_{k=1}^Nb_ky(n-k)

一个信号可以用脉冲信号的和表示：

x(n)=∑k=−∞+∞x(k)δ(n−k)x(n)=\sum\limits_{k=-\infty}^{+\infty}x(k)\delta(n-k)

由于δ(n)\delta(n)在系统中的响应是h(n)h(n)，根据系统的线性时不变性可知

y(n)=∑k=−∞+∞x(k)h(n−k)=x(n)∗h(n)y(n)=\sum\limits_{k=-\infty}^{+\infty}x(k)h(n-k)=x(n)*h(n)

这是从滤波器角度对时域卷积定理的解释。根据滤波器的含义显然有

Y(ω)=X(ω)H(ω)Y(\omega)=X(\omega)H(\omega)

例 线性时不变系统的稳定的的充要条件是：

∑n=−∞+∞∣h(n)∣=P<+∞\sum\limits_{n=-\infty}^{+\infty}|h(n)|=P<+\infty

证明：充分性

设系统输入有界，即

∣x(n)∣<B, ∀n|x(n)|<B,\ \forall n

根据线性时不变系统的性质

∣y(n)∣=∣∑k=−∞+∞x(k)h(n−k)∣≤∑k=−∞+∞∣x(k)h(n−k)∣|y(n)|=\left|\sum\limits_{k=-\infty}^{+\infty}x(k)h(n-k)\right|\leq\sum\limits_{k=-\infty}^{+\infty}|x(k)h(n-k)|

≤∑k=−∞+∞B∣h(n−k)∣=B∑k=−∞+∞∣h(n−k)∣=BP\leq\sum\limits_{k=-\infty}^{+\infty}B|h(n-k)|=B\sum\limits_{k=-\infty}^{+\infty}|h(n-k)|=BP

即系统稳定

证明：必要性

假设系统稳定，但

∑n=−∞+∞∣h(n)∣=+∞\sum\limits_{n=-\infty}^{+\infty}|h(n)|=+\infty

则构造以下系统激励

x(n)={0h(−n)=0h∗(−n)∣h(−n)∣h(−n)≠0x(n)=\begin{cases}0 & h(-n)=0\\ \frac{h^*(-n)}{|h(-n)|} & h(-n)\neq0\end{cases}

则

y(0)=∑k=−∞+∞x(k)h(−k)=∑k=−∞+∞∣h(−k)∣=+∞y(0)=\sum\limits_{k=-\infty}^{+\infty}x(k)h(-k)=\sum\limits_{k=-\infty}^{+\infty}|h(-k)|=+\infty

与系统稳定矛盾

脉冲响应的用途：系统串联

假设两个系统串联，即

x(n)⟶h1(n)⟶h2(n)y(n)x(n)\stackrel{h_1(n)}\longrightarrow\stackrel{h_2(n)}\longrightarrow y(n)

则

y(n)=h2(n)∗[h1(n)∗x(n)]=[h1(n)∗h2(n)]∗x(n)y(n)=h_2(n)*[h_1(n)*x(n)]=[h_1(n)*h_2(n)]*x(n)

根据卷积的交换律，这和

x(n)⟶h2(n)⟶h1(n)y(n)x(n)\stackrel{h_2(n)}\longrightarrow\stackrel{h_1(n)}\longrightarrow y(n)

x(n)⟶h1(n)∗h2(n)y(n)x(n)\stackrel{h_1(n)*h_2(n)}\longrightarrow y(n)

等效

即：串联系统的等效脉冲响应是子系统脉冲响应的卷积

系统并联：将x(n)x(n)经过h1(n)h_1(n)和h2(n)h_2(n)的响应相加得到y(n)y(n)，显然系统的等效脉冲响应是

h1(n)+h2(n)h_1(n)+h_2(n)

系统的频率响应：表示系统对激励中各频率分量的幅度和相位影响

回忆：

Y(ω)=X(ω)H(ω)Y(\omega)=X(\omega)H(\omega)

因此系统的频率响应H(ω)H(\omega)就是对输入对应频率分量的选择

频响通常是复值函数：

H(ω)=∣H(ω)∣ejϕ(ω)H(\omega)=|H(\omega)|e^{j\phi(\omega)}

其中∣H(ω)∣|H(\omega)|称为幅频响应，jϕ(ω)j\phi(\omega)称为相频响应

接下来我们从差分方程的角度考虑滤波器的频率响应，考虑差分方程：

∑k=0Nb(k)y(n−k)=∑r=0Ma(r)x(n−r)\sum\limits_{k=0}^{N}b(k)y(n-k)=\sum\limits_{r=0}^{M}a(r)x(n-r)

由于DTFT是线性变换，我们可以对两边同时取DTFT，得到的结果仍然相等

首先考虑

DTFT[b(k)y(n−k)]=b(k)∑n=−∞+∞y(n−k)e−jnω{\rm DTFT}[b(k)y(n-k)]=b(k)\sum\limits_{n=-\infty}^{+\infty}y(n-k)e^{-jn\omega}

=b(k)Y(ω)e−jkω=b(k)Y(\omega)e^{-jk\omega}

于是

Y(ω)∑k=0Nb(k)e−jkω=X(ω)∑r=0Ma(r)e−jrωY(\omega)\sum\limits_{k=0}^Nb(k)e^{-jk\omega}=X(\omega)\sum\limits_{r=0}^Ma(r)e^{-jr\omega}

于是

H(ω)=Y(ω)X(ω)=∑r=0Ma(r)e−jrω∑k=0Nb(k)e−jkωH(\omega)=\frac{Y(\omega)}{X(\omega)}=\frac{\sum\limits_{r=0}^Ma(r)e^{-jr\omega}}{\sum\limits_{k=0}^Nb(k)e^{-jk\omega}}

类似地，我们讨论系统串联和并联时的等效频响，根据DTFT的性质显然有

串联：

H(ω)=H1(ω)H2(ω)H(\omega)=H_1(\omega)H_2(\omega)

并联：

H(ω)=H1(ω)+H2(ω)H(\omega)=H_1(\omega)+H_2(\omega)