属性文法

在上下文无关语言的基础上，为每个文法符号关联属性(Attribute)，并且为每个产生式关联一个语义规则集合或语义动作

属性可以是任何与文法符号相关的特性，文法符号 $X$ 的属性 $a$ 用 $X.a$ 表示

属性文法中，使用语义规则来访问、改写属性，其简单的形式为覆写，例如：

X.a:=Y.b

更加复杂的形式可以涉及语义函数，即产生式中各个文法符号的属性的函数：

b:=f(c_1,c_2,...,c_k)

根据上面的语义规则，可以将属性 $b$ 分为两类：

综合属性： $b$ 是产生式左侧符号的属性
继承属性： $b$ 是产生式右侧某个符号的属性

属性文法的一个简单例子如下：

S\to E,\ \{\mathrm{ print}(E.{\rm val})\}

E\to E_1+E_2,\ \{E.{\rm val}=E_1.{\rm val}+E_2.{\rm val}\}

E\to d,\ \{E.{\rm val}=d.{\rm lexval}\}

这展示了对于一个纯加法表达式，由词法分析得到的属性 $\rm lexval$ 计算表达式结果的过程

注意，上面文法中 $E_1$ 和 $E_2$ 均代表非终结符 $E$ ，引入下标只是为了对来自不同非终结符的属性进行区分

上述属性文法只含有综合属性，可以通过自底向上遍历语法分析树（即归约）直接计算出表达式的结果，也即：在语法分析的同时完成了语义计算，这就是所谓“语法制导的语义计算”中制导的含义

然而，属性文法可能不止含有综合属性，对于含有继承属性的情况，难以在简单的归约分析过程中完成全部语义计算

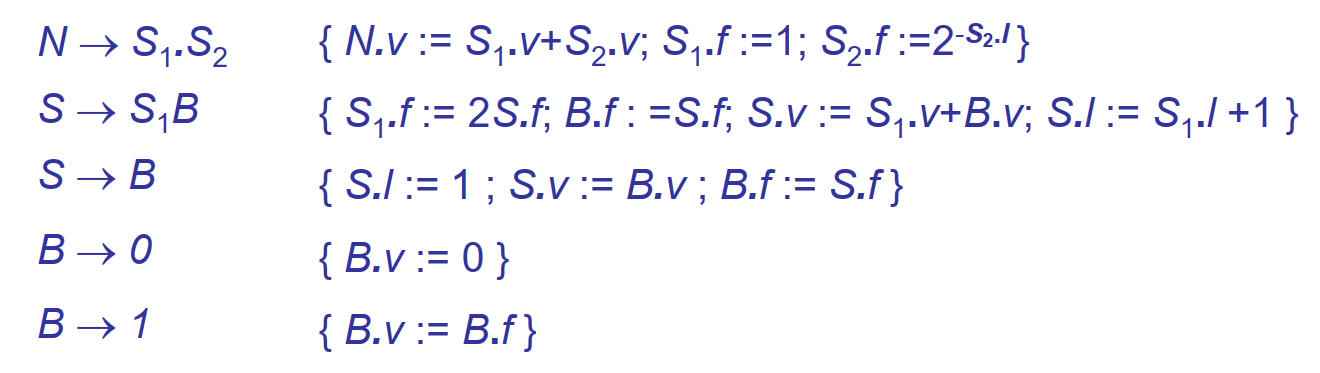
例如对上述同时含有综合属性和继承属性的文法（开始符号为 $N$ ），它的语义功能为计算二进制小数的值，具体属性含义如下：

$I$ 表示符号对应串的位数
$f$ 表示符号对应串的最低位位权，即整个串求值时乘以的倍率
$v$ 表示符号对应串的求值（已考虑位权的情况下）

上述属性文法可以采取以下的计算顺序：

自底向上计算小数部分的 $I$
由起始产生式计算出小数部分的位权 $f$
自顶向下传递位权 $f$
自底向上计算符号的 $v$
由起始产生式拼接整数部分和小数部分

这经历了一个相对复杂的多遍遍历过程

基于属性文法的语义计算

树遍历方法

树遍历方法的具体步骤如下：

构造语法分析树
构造各个属性之间的依赖图
如果依赖图无环，则可以对该图进行拓扑排序，以此顺序遍历分析树即可计算所有的属性

如果依赖图有环，则属性文法不是良定义的，即它的属性值可能存在因循环依赖而无法确定的情况

关于有向无环图(DAG)和拓扑排序可以参考拓扑排序 - OI Wiki

依赖图的构造

依赖图构造算法为

对分析树中的每一个节点
1. 为该节点所用产生式中每个语义规则涉及的属性建立节点
2. 为该节点所用产生式中每个无返回语义函数（形如 $f(c_1,c_2,...,c_k)$ ，但并未覆写某个属性）建立节点，这种节点被称为虚节点
对分析树中每一个节点的产生式中的每一条语义规则 $b:=f(c_1,c_2,...,c_k)$ $b := f (c_{1}, c_{2}, ..., c_{k})$
1. 若语义规则为无返回的语义函数，则 $b$ 视为该函数的虚节点
2. 从每个 $c_i$ 向 $b$ 建立有向边

树遍历方法的能力和不足

从上面的讨论可以看出，树遍历方法可以对任何良定义的属性文法进行语义计算，得到的结果为带标注的(annotated)语法分析树

然而，树遍历方法可能会对很多节点进行多次遍历，并且往往需要先生成语法分析树再进行遍历，复杂度较高

正如我们希望语法分析过程能够单遍完成一样（为此我们研究了诸如LL(1)，LR(0)，LR(1)等语法分析方法），我们同样希望语义计算可以单遍完成，但这自然会对属性文法做出约束

单遍方法

我们对属性文法做出以下约束：

S-属性文法：只含综合属性
L-属性文法：可以同时包含综合属性和继承属性，但
- 任何继承属性的计算只取决于该属性所属的符号左边的符号的属性

S-属性文法的语义计算

可以利用LR分析技术，自底向上进行，具体地：

扩充分析栈，使之包含存放综合属性值的语义栈
在决定利用产生式归约的时刻进行语义计算

L-属性文法的语义计算

利用LL分析技术，在推导时计算每个右端符号的继承属性，在完成每个右端符号的分析时计算左端符号的综合属性

基于翻译模式的语义计算

翻译模式是一种比属性文法在计算顺序上更加严格的描述方式，具体地：

与属性文法相同，使用在文法的基础上附加花括号标出的语义规则集的形式
与属性文法不同的是，语义规则集可以出现在产生式右端任何位置，可以显式表示计算次序

与属性文法类似，翻译模式需要受到一定的限制才可以单遍分析，具体地：

类似S-属性文法，仅包含综合属性，且对综合属性的计算放在产生式末尾
类似L-属性文法，既包含继承属性又包含综合属性，但每个符号继承属性的计算必须在到达该符号之前，且计算式只访问左侧符号的属性；综合属性的计算放在产生式尾部

下面是一个翻译模式的例子，它对应于之前的二进制小数值计算的属性文法：

自顶向下语义计算

自顶向下的预测分析程序中，只需要在翻译模式中语义规则集对应的位置插入语义计算的指令即可

值得注意的是：

原先的parseS函数将以S的综合属性作为返回值，以其继承属性作为函数参数
自顶向下语义计算使用LL(1)方法，故有时需要消除左递归，在消除左递归时需要对语义规则集进行一些调整

翻译模式的左递归消除

考虑以下左递归的翻译模式：

A\to A_1Y\ \{A.a:=g(A_1.a,Y.y)\}

A\to X\ \{A.a:=f(X.x)\}

则句型 $XY_1Y_2$ 的语法分析树如下：

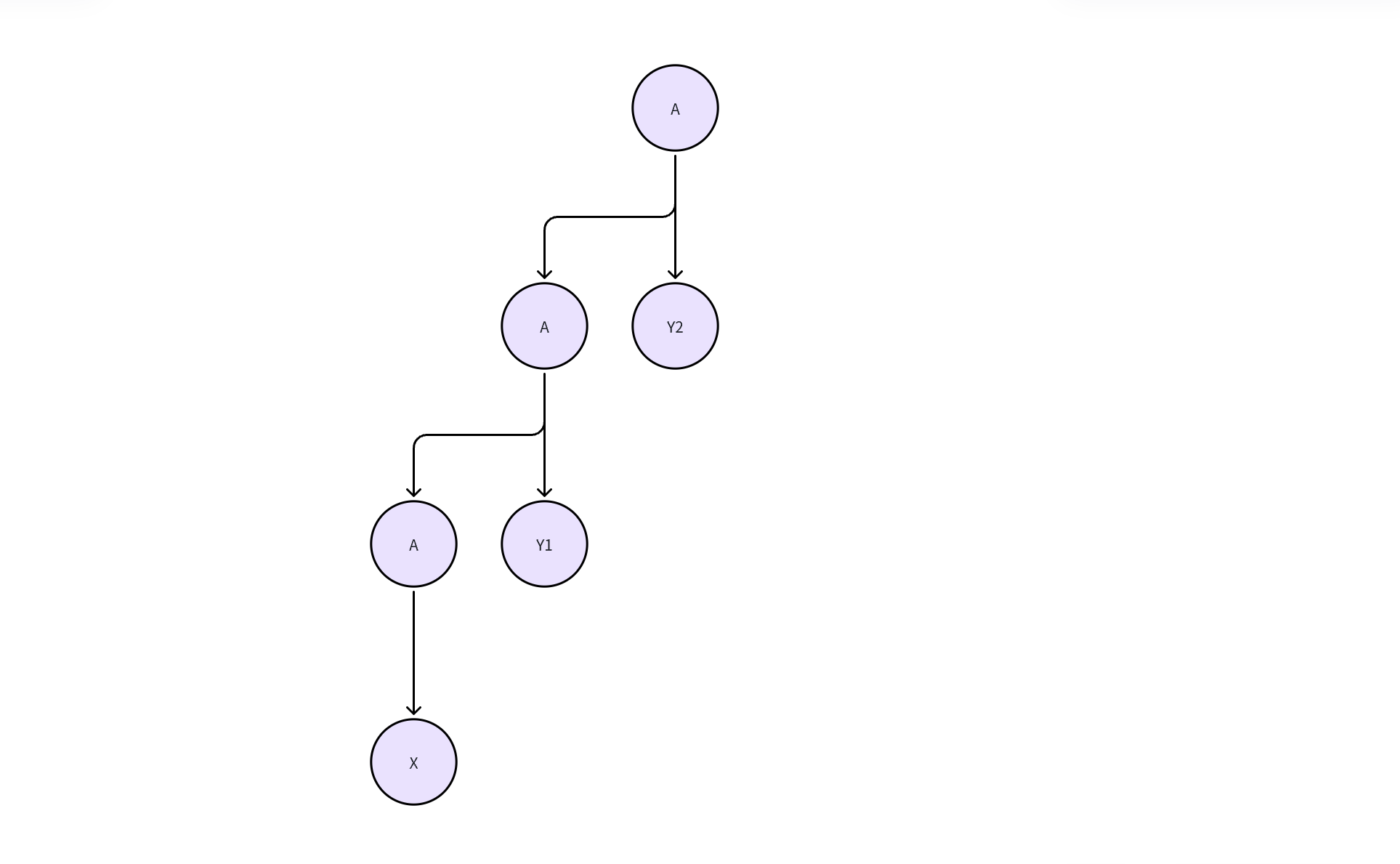
综合属性的计算发生在每个推导结束时

然而，消除左递归将文法变为

A\to XR

R\to YR\mid \epsilon

则语法分析树变为下图中右侧的结果：

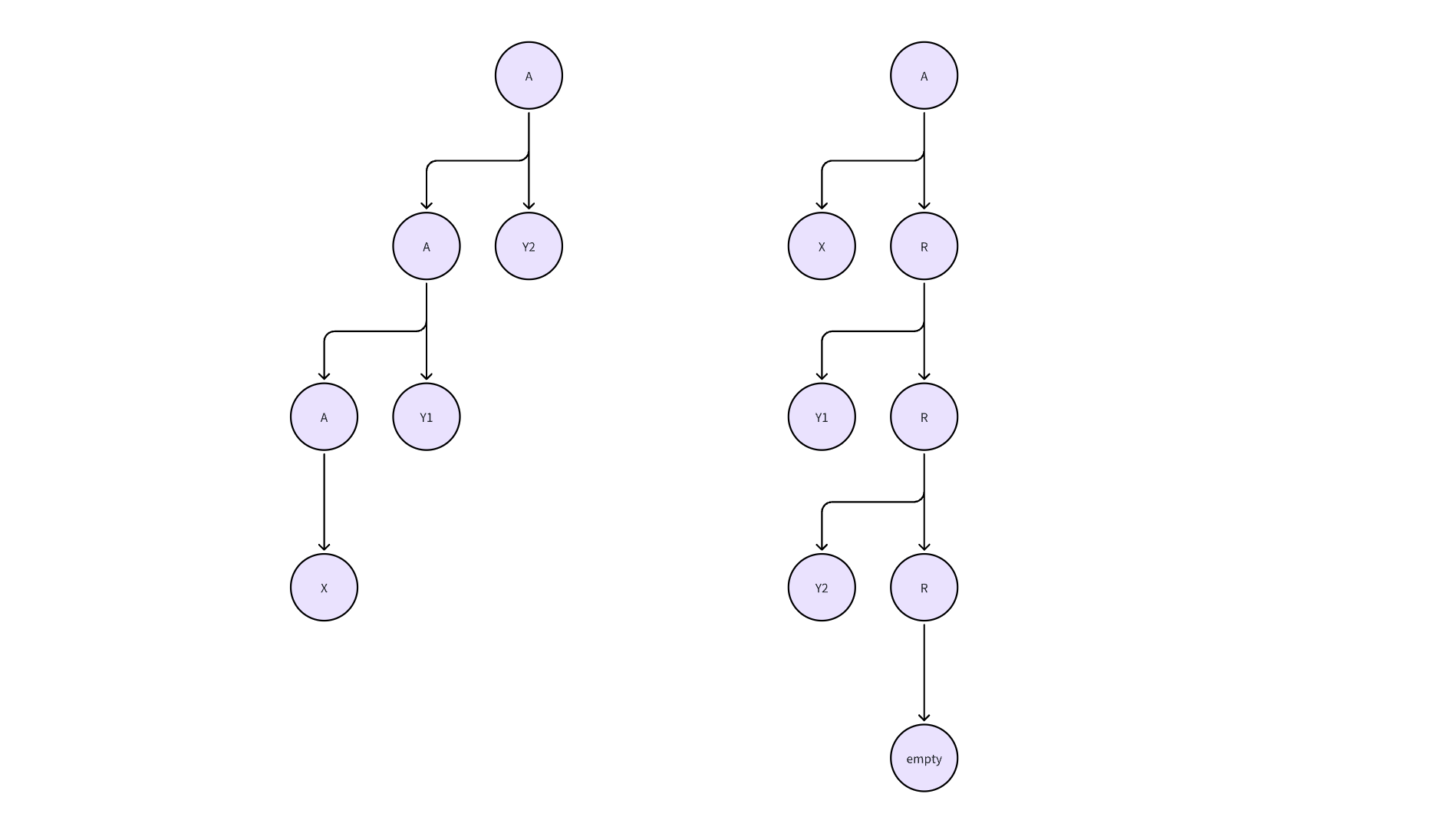
注意到这其实是对原先的树进行了一个类似数据结构中Splay的操作，此时 $X$ 、 $Y_1$ 、 $Y_2$ 在树中的高低位置反转

为此，原先以综合属性的形式计算的 $A$ 的属性在右图中必须作为 $R$ 的继承属性 $i$ ，并且在达到树底的时候再以综合属性 $s$ 的形式将 $R$ 的属性上传，回到 $A$

于是，消除左递归后的翻译模式如下：

A\to X\ \{R.i:=f(X.x)\}\ R\ \{A.a:=R.s\}

R\to Y\ \{R_1.i:=g(R.i,Y.y)\}\ R_1\ \{R.s:=R_1.s\}

R\to\epsilon\ \{R.s:=R.i\}

注意到综合属性 $s$ 只起到了将属性值从底部传回顶端的作用，而 $R.i:=f(X.x)$ 和 $R_1.i:=g(R.i,Y.y)$ 则是对原先翻译模式中 $A.a$ 的模拟

事实上，原始翻译模式中的 $A.a$ 表示的是其子树的属性；而新翻译模式的 $R.i$ 表示的是其所有左侧枝（左侧兄弟和所有祖先的左侧兄弟）的属性

自底向上语义计算

L-翻译模式的自底向上计算比较复杂，介绍以下三个方面：

去掉嵌在产生式中间的语义动作
分析栈中继承属性的访问和继承属性的模拟求值
用综合属性替代继承属性

在这三个方面中，我们会涉及一些相当简单的例子的讨论

去掉嵌在产生式中间的语义动作

动机：由于LR分析在读入短语后才具有选择归约产生式的能力，因此LR分析不能执行产生式中间的语义动作

做法非常简单：将产生式中间的语义动作用非终结符 $N$ 代替，同时加入产生式 $N\to\epsilon$ ，将上面去掉的语义动作放在这个产生式的末尾

例如：

A\to a\ \{\rm print('a')\}\ A

A\to\epsilon

改为

A\to aNA

N\to\epsilon\ \{\rm print('a')\}

A\to\epsilon

分析栈中继承属性的访问

动机：上面的步骤可以简单地处理不涉及继承属性的内嵌语义动作，但当语义动作涉及左侧符号的继承属性时，问题会变得比较复杂——这是因为LR分析通过分析栈存放属性，但语义动作计算出的继承属性属于一个不存在于栈中且不一定会马上入栈的符号（与之相比，综合属性所属的符号会在归约后马上入栈，因此可以将计算出的综合属性入栈）

考虑以下翻译模式：

D\to T\ \{L.i:=T.s\}\ L

L\to \{L_1.i:=L.i\}\ L_1,v\ \{\mathrm{foo}(L.i)\}

L\to v\ \{\mathrm{foo}(L.i)\}

注意到：

这里所有场景下出现的 $L.i$ 都等于开始的综合属性 $T.s$
每次出现 $\rm foo$ $foo$ 函数对 $L.i$ $L . i$ 的引用， $L.i$ $L . i$ 都在栈上某个固定的位置，用 $\rm top$ $top$ 表示栈顶指针，则
- 对产生式2， $L.i$ 就是 $*({\rm top}-3).s$
- 对产生式3， $L.i$ 就是 $*({\rm top}-1).s$

即：我们使用栈上相对栈顶指针的深度一定的某个符号的综合属性来替代语义规则中引用的难以寻址的继承属性

在生成分析程序时， $\rm foo$ 函数的参数并不直接传入捉摸不定的 $L.i$ ，而是传入上述的由 $\rm top$ 指针指向的综合属性 $s$

继承属性的模拟求值

动机：上面的做法局限性很大，体现在——要求每个被引用的继承属性都能用某个栈上固定深度的综合属性表示；但这对很多翻译模式并不现实

例如，考虑以下的翻译模式：

S\to aA\ \{C.i:=A.s\}\ C

S\to bAB\ \{C.i:=A.s\}\ C

C\to c\ \{C.s:=g(C.i)\}

注意到，在函数 $g$ 引用 $C.i$ 时， $C.i$ 总是体现为某个 $A.s$ ，但这里的 $A.s$ 可能在 $\rm top-1$ （对产生式1），也可能在 $\rm top-2$ （对产生式2），而产生式1和产生式2

我们希望让这里的 $A.s$ 总是存在于 $\rm top-1$ ，为此，需要在产生式2的 $B$ 后面引入新的虚拟非终结符 $M$ ，具体如下：

S\to aA\ \{C.i:=A.s\}\ C

S\to bAB\ \{M.i:=A.s\}\ M\ \{C.i:=M.s\}\ C

C\to c\ \{C.s:=g(C.i)\}

M\to\epsilon\ \{M.s:=M.i\}

于是，对产生式2， $C.i$ 改为使用 $M.s$ 而不是 $A.s$ ，解决了上面的问题

然而，上面只解决了引用的继承属性位置不确定的情况，但还可能出现引用的继承属性不在栈上的情况，即继承属性并不直接等于某个综合属性，具体例子如下：

S\to aA\ \{C.i:=f(A.s)\}\ C

这里的 $C.i$ 虽然由栈上属性 $A.s$ 决定，但 $f(A.s)$ 并不真实存在于栈上

将翻译模式改为：

S\to aA\ \{M.i:=A.s\}\ M\ \{C.i:=M.s\}\ C

M\to\epsilon\ \{M.s:=f(M.i)\}

就解决了这一问题，即引入虚拟非终结符 $M$ 用来存储 $f(A.s)$

总结

上面几个部分中，最重要的策略就是引入虚拟非终结符

虚拟非终结符是我自创的词汇，它表示那些没有语法功能（即唯一产生式是 $X\to\epsilon$ ）但有语义功能（即承担内嵌语义动作消除或继承属性定址等方便LR分析器进行语义计算的功能）

然而，更聪明的办法或许是直接修改翻译模式，使继承属性变成综合属性