连续时间情形的FT具有理论意义，但现实情况下的信号往往没有解析表达式，也无法获知任意时刻t∈Rt\in\mathbb{R}的信息

因此，将时间域离散化是必要的，这相当于以TsT_s周期进行采样

DTFT与IDTFT

回忆FT与IFT：

F(ω)=F[f(t)]=∫−∞+∞f(t)e−jωtdtF(\omega) = \mathcal{F}[f(t)] = \int_{-\infty}^{+\infty}f(t)e^{-j\omega t}{\rm d}t

f(t)=F−1[F(ω)]=12π∫−∞+∞F(ω)ejωtdωf(t) = \mathcal{F}^{-1}[F(\omega)] = \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{j\omega t}{\rm d}\omega

在实际应用中，无法取得连续的信号函数值，因此，我们使用f(nT)f(nT)作为用来进行Fourier变换的原料

于是，对FT的积分公式离散化，得到离散时间的FT：

F^(ω)=∑n=−∞+∞f(nT)e−jωnT\hat{F}(\omega)=\sum\limits_{n=-\infty}^{+\infty}f(nT)e^{-j\omega nT}

这实际上是离散时间FT函数F^(ω)\hat{F}(\omega)的一个FS，其对应的周期为2πT=ωs\frac{2\pi}{T}=\omega_s（注意：这里求FS的函数以ω\omega为自变量，需要交换ω\omega和tt来理解）

于是，对应的求FS的积分公式为：

f(nT)=1ωs∫−ωs/2ωs/2F^(ω)ejωnTdωf(nT)=\frac{1}{\omega_s}\int_{-\omega_s/2}^{\omega_s/2}\hat{F}(\omega)e^{j\omega nT}{\rm d}\omega

接下来，为了让TT和ωs\omega_s的值不影响讨论，进行频率归一化，即：

将时间域变为数字域，则f(t)f(t)变为x(n)x(n)，将采样频率固定为单位11，则ωs=2π\omega_s=2\pi，根据采样定理，可以表示的角频率范围为−π∼π-\pi\sim\pi

于是，离散时间傅里叶变换(DTFT) 定义如下：

X(ω)=DTFT[x(n)]=∑n=−∞+∞x(n)e−jωnX(\omega) = {\rm DTFT}[x(n)] = \sum\limits_{n=-\infty}^{+\infty}x(n)e^{-j\omega n}

对应的逆变换为

x(n)=IDTFT[X(ω)]=12π∫n=−ππX(ω)ejωndωx(n) = {\rm IDTFT}[X(\omega)] = \frac{1}{2\pi}\int_{n=-\pi}^{\pi}X(\omega)e^{j\omega n}{\rm d}\omega

注意，归一化后ω\omega和之前的ω\omega的含义已经发生了变化

数字频率与模拟频率

上述数字域信号经过了时间的归一化，即将一个采样周期定义为数字域的“时间”11

因此，数字域的频率ω\omega并不是真实频率

我们用Ω\Omega表示模拟频率（量纲为Hz\rm Hz），即模拟时间域下的频率，用ω\omega表示数字频率（量纲为11）

例如，模拟频率的Nyquist区间（即可以从采样还原的频率区间）为[−Ωs/2,Ωs/2][-\Omega_s/2, \Omega_s/2]

二者换算关系如下：

Ω=ωfs\Omega = \omega f_s

注 DTFT本质上经过了采样，因此DTFT的结果永远是频域上周期的

DTFT的性质

DTFT的频谱密度函数是周期函数

X(ω)=X(ω+2π)X(\omega)=X(\omega+2\pi)

DTFT是线性变换

DTFT[λf+μg]=λDTFT[f]+μDTFT[g]{\rm DTFT}[\lambda f+\mu g]=\lambda{\rm DTFT}[f]+\mu{\rm DTFT}[g]

DTFT继承FT的平移特性

  • 时移：DTFT[x(n−n0)]=e−jωn0X(ω), n0∈Z{\rm DTFT}[x(n-n_0)]=e^{-j\omega n_0}X(\omega),\ n_0\in\Z
  • 频移：DTFT[ejω0nx(n)]=X(ω−ω0){\rm DTFT}[e^{j\omega_0n}x(n)]=X(\omega-\omega_0)

DTFT继承FT的反褶、共轭特性

  • 反褶：DTFT[x(−n)]=X(−ω){\rm DTFT}[x(-n)]=X(-\omega)
  • 共轭：DTFT[x∗(n)]=X∗(−ω){\rm DTFT}[x^*(n)]=X^*(-\omega)

DTFT的时域扩展：对于

x(a)(n)={x(na)na∈Z0else, a∈Z,a≠0x_{(a)}(n)=\begin{cases}x(\frac{n}{a}) & \frac{n}{a}\in\Z \\ 0 & {\rm else}\end{cases},\ a\in\Z, a\neq 0

则

X(a)(ω)=X(aω)X_{(a)}(\omega)=X(a\omega)

这里只讨论了时域扩展，却没有讨论以x(2n)x(2n)为例的时域压缩，这里进行一个简单的讨论

由于数字域信号限制定义域为Z\Z，因此x(n/2)x(n/2)和x(2n)x(2n)各会遇到一些问题：

  • 对于y(n)=x(n/2)y(n)=x(n/2)而言，n/2n/2有时会落在x(n)x(n)定义域之外，因此需要使用上面的方法强行使定义域之外的函数值为00，得到x(2)(n)x_{(2)}(n)的定义
  • 对于y(n)=x(2n)y(n)=x(2n)而言，虽然定义上没有问题，但由于y(1/2)y(1/2)对y(n)y(n)没有意义，原来信号中x(1)x(1)的值在压缩过程中被丢失了（丢失的还有所有其他奇数项）

然而，我们实际上可以从X(ω)X(\omega)得到DTFT[x(2n)]{\rm DTFT}[x(2n)]的表达式，先看下面的例子：

由于

X(ω)=∑n=−∞+∞x(n)e−jnωX(\omega)=\sum\limits_{n=-\infty}^{+\infty}x(n)e^{-jn\omega}

可以得到

X(0)=∑n=−∞+∞x(n)X(0)=\sum\limits_{n=-\infty}^{+\infty}x(n)

X(π)=∑n=−∞+∞x(n)e−jnπ=∑n=−∞+∞(−1)nx(n)X(\pi)=\sum\limits_{n=-\infty}^{+\infty}x(n)e^{-jn\pi}=\sum\limits_{n=-\infty}^{+\infty}(-1)^nx(n)

于是可以求出x(n)x(n)的偶数项和

∑n=−∞+∞x(2n)=X(0)+X(π)2\sum\limits_{n=-\infty}^{+\infty}x(2n)=\frac{X(0)+X(\pi)}{2}

接下来我们让ω\omega变起来，考虑

X(ω)=∑n=−∞+∞x(n)e−jnωX(\omega)=\sum\limits_{n=-\infty}^{+\infty}x(n)e^{-jn\omega}

X(ω+π)=∑n=−∞+∞x(n)e−jnωe−jnπ=∑n=−∞+∞(−1)nx(n)e−jnωX(\omega+\pi)=\sum\limits_{n=-\infty}^{+\infty}x(n)e^{-jn\omega}e^{-jn\pi}=\sum\limits_{n=-\infty}^{+\infty}(-1)^nx(n)e^{-jn\omega}

于是

X(ω)+X(ω+π)2=∑n=−∞+∞x(2n)e−j(2n)ω\frac{X(\omega)+X(\omega+\pi)}{2}=\sum\limits_{n=-\infty}^{+\infty}x(2n)e^{-j(2n)\omega}

进而

DTFT[x(2n)]=∑n=−∞+∞x(2n)e−jnω=X(ω/2)+X(ω/2+π)2{\rm DTFT}[x(2n)]=\sum\limits_{n=-\infty}^{+\infty}x(2n)e^{-jn\omega}=\frac{X(\omega/2)+X(\omega/2+\pi)}{2}

类似地，我们可以得到DTFT[x(an+b)], a∈Z+,b∈Z{\rm DTFT}[x(an+b)],\ a\in\Z_+,b\in\Z的表达式

令λk\lambda_k为第kk个aa次单位根，即

λk=ej2kπa, k=0,1,...,a−1\lambda_k=e^{j\frac{2k\pi}{a}},\ k=0,1,...,a-1

则计算以下频移：

X(ω+2kπa)=∑n=−∞+∞x(n)e−jnωe−jn2kπa=∑n=−∞+∞λknx(n)e−jnωX(\omega+\frac{2k\pi}{a})=\sum\limits_{n=-\infty}^{+\infty}x(n)e^{-jn\omega}e^{-jn\frac{2k\pi}{a}}=\sum\limits_{n=-\infty}^{+\infty}\lambda_k^nx(n)e^{-jn\omega}

两边同乘1/λbk1/\lambda_b^k，

1λbkX(ω+2kπa)=∑n=−∞+∞λknλbkx(n)e−jnω\frac{1}{\lambda_b^k}X(\omega+\frac{2k\pi}{a})=\sum\limits_{n=-\infty}^{+\infty}\frac{\lambda_k^n}{\lambda_b^k}x(n)e^{-jn\omega}

将λk\lambda_k中kk的取值范围修改为全体整数，即：

λk=ej2kπa, k∈Z\lambda_k=e^{j\frac{2k\pi}{a}},\ k\in\Z

则上式修改为

λ−kbX(ω+2kπa)=∑n=−∞+∞λk(n−b)x(n)e−jnω\lambda_{-kb}X(\omega+\frac{2k\pi}{a})=\sum\limits_{n=-\infty}^{+\infty}\lambda_{k(n-b)}x(n)e^{-jn\omega}

将上面的式子对k=0,1,...,a−1k=0,1,...,a-1叠加，

(∑k=0a−1λ−kbX(ω+2kπa))=∑n=−∞+∞(∑k=0a−1λk(n−b))x(n)e−jnω\left(\sum\limits_{k=0}^{a-1}\lambda_{-kb}X(\omega+\frac{2k\pi}{a})\right)=\sum\limits_{n=-\infty}^{+\infty}\left(\sum\limits_{k=0}^{a-1}\lambda_{k(n-b)}\right)x(n)e^{-jn\omega}

接下来考虑上式右端的系数Cn=∑k=0a−1λk(n−b)C_n=\sum\limits_{k=0}^{a-1}\lambda_{k(n-b)}

当a∣k−ba\mid k-b时，设n=qa+b, q∈Zn=qa+b,\ q\in\Z

Cn=∑k=0a−1λkqa=∑k=0a−11=aC_n=\sum\limits_{k=0}^{a-1}\lambda_{kqa}=\sum\limits_{k=0}^{a-1}1=a

而当a∤k−ba\nmid k-b时，设n=qa+b+r, q∈Z, r∈{0,1,...,a−1}n=qa+b+r,\ q\in\Z,\ r\in\{0,1,...,a-1\}

Cn=∑k=0a−1λkqa+kr=∑k=0a−1λkrC_n=\sum\limits_{k=0}^{a-1}\lambda_{kqa+kr}=\sum\limits_{k=0}^{a-1}\lambda_{kr}

设gcd⁡(r,a)=d, r/d=rd, a/d=ad\gcd(r,a)=d,\ r/d=r_d,\ a/d=a_d，有gcd⁡(rd,ad)=1\gcd(r_d,a_d)=1，则

Cn=∑k=0a−1ej2krπa=∑k=0a−1ej2krdπad=d∑k=0ad−1ej2krdπadC_n=\sum\limits_{k=0}^{a-1}e^{j\frac{2kr\pi}{a}}=\sum\limits_{k=0}^{a-1}e^{j\frac{2kr_d\pi}{a_d}}=d\sum\limits_{k=0}^{a_d-1}e^{j\frac{2kr_d\pi}{a_d}}

右侧最后一项求和式为ada_d次单位根的求和，根据单位根的性质该和式为零，故

Cn={a,a∣n−b0,a∤n−bC_n=\begin{cases}a,&a\mid n-b\\0,&a\nmid n-b\end{cases}

于是前面得到的等式可以改写为

(∑k=0a−1λ−kbX(ω+2kπa))=∑n=−∞+∞ax(an+b)e−j(an+b)ω=ae−jbωDTFT[x(an+b)](aω)\left(\sum\limits_{k=0}^{a-1}\lambda_{-kb}X(\omega+\frac{2k\pi}{a})\right)=\sum\limits_{n=-\infty}^{+\infty}ax(an+b)e^{-j(an+b)\omega}=ae^{-jb\omega}{\rm DTFT}[x(an+b)](a\omega)

于是

DTFT[x(an+b)]=1aejbωa∑k=0a−1X(ω+2kπa)λkb{\rm DTFT}[x(an+b)]=\frac{1}{a}e^{j\frac{b\omega}{a}}\sum\limits_{k=0}^{a-1}\frac{X(\frac{\omega+2k\pi}{a})}{\lambda_k^b}

事实上，我们也可以定义一个这个问题的“窗函数”，即：

w(n)={1,a∣n−b0,a∤n−bw(n)=\begin{cases}1,&a\mid n-b\\0,&a\nmid n-b\end{cases}

则

W(ω)=∑n=−∞+∞w(n)e−jnω=∑n=−∞+∞e−j(an+b)ωW(\omega)=\sum\limits_{n=-\infty}^{+\infty}w(n)e^{-jn\omega}=\sum\limits_{n=-\infty}^{+\infty}e^{-j(an+b)\omega}

但此窗函数与X(ω)X(\omega)进行圆周卷积似乎不太容易计算

DTFT的频域微分：

DTFT[nx(n)]=j[ddωX(ω)]{\rm DTFT}[nx(n)]=j\Big[\frac{\rm d}{\rm d\omega}X(\omega)\Big]

DTFT的时域卷积：

DTFT[x1(n)∗x2(n)]=X1(ω)⋅X2(ω){\rm DTFT}[x_1(n)*x_2(n)]=X_1(\omega)\cdot X_2(\omega)

其中，离散卷积的定义如下：

x1(n)∗x2(n)=∑k=−∞+∞x1(n−k)x2(k)x_1(n)*x_2(n)=\sum\limits_{k=-\infty}^{+\infty}x_1(n-k)x_2(k)

DTFT的频域卷积：

DTFT[x1(n)⋅x2(n)]=12πX1(ω)⊗X2(ω){\rm DTFT}[x_1(n)\cdot x_2(n)]=\frac{1}{2\pi}X_1(\omega)\otimes X_2(\omega)

其中，圆周卷积的定义如下：

X1(ω)⊗X2(ω)=∫−ππX1(ω′)X2(ω−ω′)dω′X_1(\omega)\otimes X_2(\omega)=\int_{-\pi}^\pi X_1(\omega')X_2(\omega-\omega'){\rm d}\omega'

DTFT的Parseval定理（能量公式）：

∑n=−∞+∞∣x(n)∣2=12π∫−ππ∣Xω(ω)∣2dω\sum\limits_{n=-\infty}^{+\infty}|x(n)|^2=\frac{1}{2\pi}\int_{-\pi}^\pi |X_\omega(\omega)|^2{\rm d}\omega

有限长DTFT

实际生产中无法获得从n=−∞n=-\infty到+∞+\infty的离散时间信号，因此需要乘以时域上的矩形窗：

w(n)={10≤n≤L−10elsew(n)=\begin{cases}1 & 0\leq n\leq L-1 \\ 0 & \rm else\end{cases}

xL(n)=x(n)w(n)x_L(n)=x(n)w(n)

角度1：直接计算xLx_L的DTFT

XL(ω)=∑n=−∞+∞xL(n)e−jnω=∑n=0L−1x(n)e−jnωX_L(\omega)=\sum\limits_{n=-\infty}^{+\infty}x_L(n)e^{-jn\omega}=\sum\limits_{n=0}^{L-1}x(n)e^{-jn\omega}

角度2：使用频域卷积定理

XL(ω)=12πX(ω)⊗W(ω)X_L(\omega)=\frac{1}{2\pi}X(\omega)\otimes W(\omega)

其中

W(ω)=∑n=−∞+∞w(n)e−jωn=∑n=0L−1e−jωnW(\omega)=\sum\limits_{n=-\infty}^{+\infty}w(n)e^{-j\omega n}=\sum\limits_{n=0}^{L-1}e^{-j\omega n}

利用等比数列求和公式

W(ω)=1−e−jωL1−e−jω=1−cos⁡Lω+jsin⁡Lω1−cos⁡ω+jsin⁡ω=2sin⁡2Lω2+2jsin⁡Lω2cos⁡Lω22sin⁡2ω2+2jsin⁡ω2cos⁡ω2W(\omega)=\frac{1-e^{-j\omega L}}{1-e^{-j\omega}}=\frac{1-\cos L\omega+j\sin L\omega}{1-\cos\omega+j\sin\omega}=\frac{2\sin^2\frac{L\omega}{2}+2j\sin\frac{L\omega}{2}\cos\frac{L\omega}{2}}{2\sin^2\frac{\omega}{2}+2j\sin\frac{\omega}{2}\cos\frac{\omega}{2}}

=sin⁡(Lω/2)sin⁡(ω/2)e−j(L−1)ω/2=\frac{\sin(L\omega/2)}{\sin(\omega/2)}e^{-j(L-1)\omega/2}

于是，窗函数的频谱幅度为

∣W(ω)∣=∣sin⁡(Lω/2)sin⁡(ω/2)∣|W(\omega)|=\left|\frac{\sin(L\omega/2)}{\sin(\omega/2)}\right|

插入讨论：离散时间Fourier变换与多缝Fraunhofer衍射

本人并不懂物理，但在学习这部分的过程中发现，在记忆中学习光的衍射时有一个公式的形式与上面推导出的W(ω)W(\omega)极其相似，经查阅，这个W(ω)W(\omega)的形式是光的多缝Fraunhofer衍射光强公式中的一项

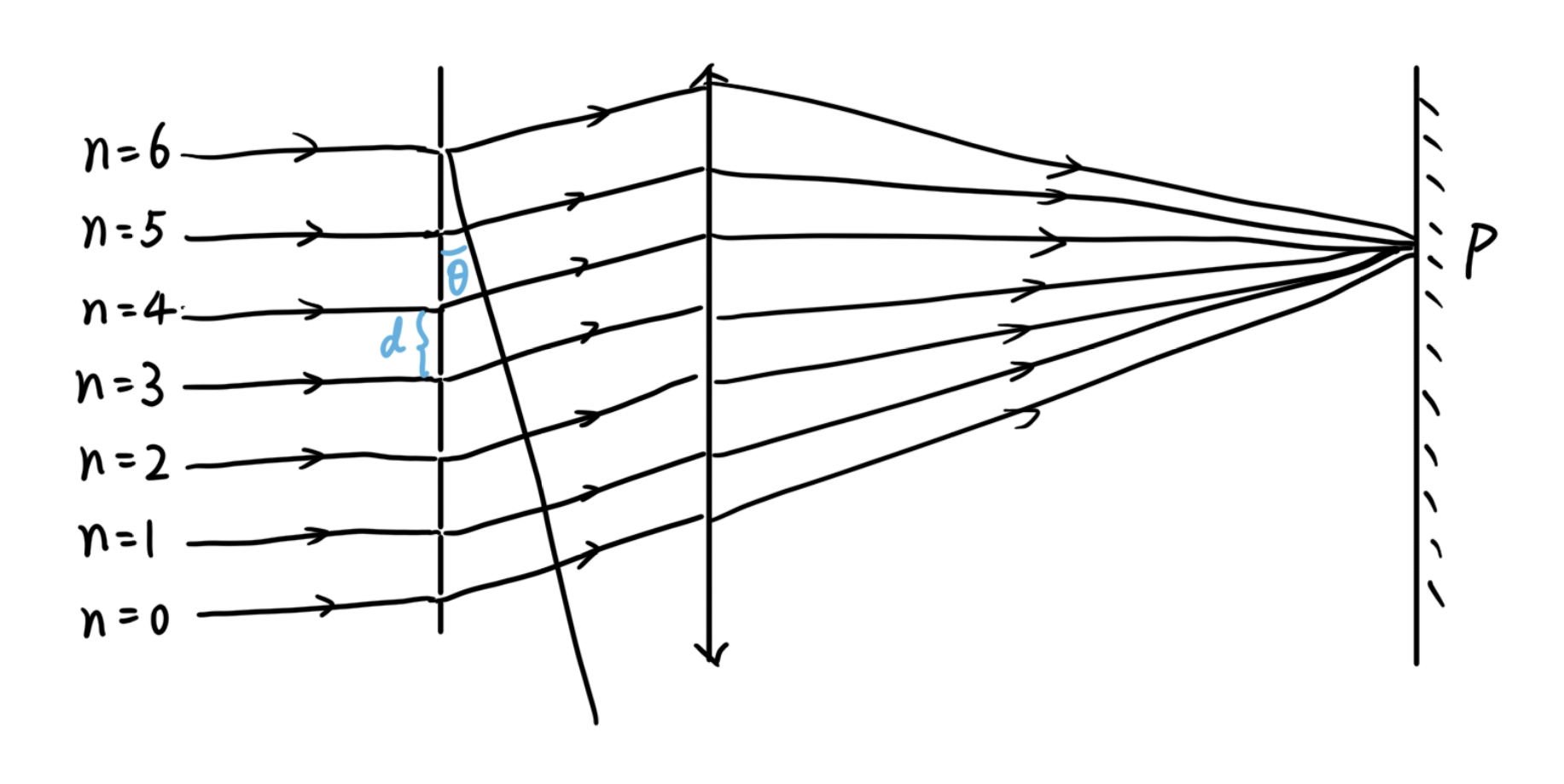
127486c8

这表示的是上面的光学问题：平行光垂直穿过一块有NN条缝（在上面的示意图中N=7N=7）的玻璃板，经过玻璃板衍射后再由凸透镜聚焦到焦面上，考虑焦面上某一点的光强

首先，由于平行光会经凸透镜会聚到焦平面上同一点，因此P点的位置唯一对应于光线离开多缝时的偏转角度θ\theta；平行光在进入多缝前相位是同步的，而透镜满足物像等光程，结论是，每束光到达P点时的相位ϕ\phi是光束编号nn的线性函数，即

ϕ=2πdsin⁡θλn+ϕ0\phi=\frac{2\pi d\sin\theta}{\lambda}n+\phi_0

此时其实已经容易看出P点各束光光矢量的和呈现出类似∑n=0N−1e−jnω\sum\limits_{n=0}^{N-1}e^{-jn\omega}的形式，但我们将用Fourier变换的语言来分析它

我们把光束的条数nn看成DTFT的数字域，那么上面问题中的信号就是我们讨论的窗函数（这里设一束光的振动幅度为11）：

w(n)={1,n=0,1,2,...,L−10,elsew(n)=\begin{cases}1, & n=0,1,2,...,L-1 \\ 0, & \rm else\end{cases}

而这个问题中的数字频率ω\omega正比于sin⁡θ\sin\theta，因为sin⁡θ\sin\theta越大，ϕ\phi随nn变化的变化率就越大，也就越快完成一个周期，事实上

ω=2πdsin⁡θλ\omega=\frac{2\pi d\sin\theta}{\lambda}

于是，要求出光矢量依P点位置（正相关于sin⁡θ\sin\theta）的分布，只需要求上面的数字域信号w(n)w(n)对ω\omega的分布，这就是Fourier变换

回归正题，由窗函数频谱，定义其主瓣宽度（即ω=0\omega=0附近的瓣的宽度的一半）为ΔωW=2π/L\Delta\omega_W=2\pi/L

下面讨论以下频谱只有两个分量的信号：

x(n)=A1ejω1n+A2ejω2n, ω1,ω2∈(0,π)x(n)=A_1e^{j\omega_1 n}+A_2e^{j\omega_2 n},\ \omega_1,\omega_2\in(0,\pi)

其频谱为

X(ω)=2π(A1δ(ω−ω1)+A2δ(ω−ω2))X(\omega)=2\pi(A_1\delta(\omega-\omega_1)+A_2\delta(\omega-\omega_2))

加窗后的频谱为

XL(ω)=12πX(ω)⊗W(ω)=A1W(ω−ω1)+A2W(ω−ω2)X_L(\omega)=\frac{1}{2\pi}X(\omega)\otimes W(\omega)=A_1W(\omega-\omega_1)+A_2W(\omega-\omega_2)

可以看出，与窗函数卷积相当于将原本是冲激信号（即清晰）的谱线进行展宽（即变得模糊，成为上面W(ω)W(\omega)的形状，下面只考虑其占据能量主要部分的主瓣），此时如果两条谱线的频率差Δω\Delta\omega满足

Δω<ΔωW\Delta\omega<\Delta\omega_W

则一条谱线的主瓣中心进入另一条谱线的主瓣，认为此时两条谱线不可分辨，即窗函数的频谱分辨率

Δωmin=ΔωW=2πL\Delta\omega_{\rm min}=\Delta\omega_W=\frac{2\pi}{L}

它无法区分频率差低于2π/L2\pi/L的谱线

讨论

  1. 加窗后，数据长度决定频谱分辨率，被称为不确定原理
    • 一个更接近物理中不确定原理的表述为LΔω≤2πL\Delta\omega\leq2\pi
    • 若L=1L=1，此时的频谱分辨率为2π2\pi，而数字频率的取值范围是(−π,π)(-\pi,\pi)，这意味着无法分辨任何频率，但事实上我们只取了一个样本点本就无法得到频率信息，这是自洽的
  2. 加窗后出现频率泄漏，这是因为W(ω)W(\omega)不光存在主瓣，还存在旁瓣，旁瓣将原有的谱线展宽到了原先不存在的高频
  3. 上面的讨论仍然与物理光学非常相似，包括对谱线分辨率的研究，而且衍射中的谱线宽度在光子数目很少的时候即表现为光子位置的不确定性