采样与量化

采样和量化的目的：把模拟信号变为数字信号

  • 采样：每隔一个时间间隔在模拟信号波形上抽取一个幅度值
  • 量化：把采样得到的幅度值用若干位二进制定点数表达

最终得到信号的理论比特率：采样频率×量化位数

采样相关的物理量用下角标s_s表示

采样的数学模型

理想采样：使用冲激串

p(t)=∑n=−∞+∞δ(t−nTs)p(t)=\sum\limits_{n=-\infty}^{+\infty}\delta(t-nT_s)

与原始信号x(t)x(t)相乘，即：

xp(t)=x(t)p(t)=∑n=−∞+∞x(nTs)δ(t−nTs)x_p(t)=x(t)p(t)=\sum\limits_{n=-\infty}^{+\infty}x(nT_s)\delta(t-nT_s)

为了从频域分析采样信号，我们需要首先分析冲激串信号p(t)p(t)的FT

P(ω)=F[p(t)]P(\omega)=\mathcal{F}[p(t)]

首先求出p(t)p(t)的FS系数

cn=1Ts∫−Ts2Ts2p(t)e−jnωstdt=1Tsc_n=\frac{1}{T_s}\int_{-\frac{T_s}{2}}^{\frac{T_s}{2}}p(t)e^{-jn\omega_st}{\rm d}t=\frac{1}{T_s}

于是p(t)p(t)的FS为

p(t)=1Ts∑n=−∞+∞ejnωstp(t)=\frac{1}{T_s}\sum\limits_{n=-\infty}^{+\infty}e^{jn\omega_st}

对上述FS求FT

P(ω)=1Ts∑n=−∞+∞F[ejnωst]=2πTs∑n=−∞+∞δ(ω−nωs)P(\omega)=\frac{1}{T_s}\sum\limits_{n=-\infty}^{+\infty}\mathcal{F}[e^{jn\omega_st}]=\frac{2\pi}{T_s}\sum\limits_{n=-\infty}^{+\infty}\delta(\omega-n\omega_s)

其中

ωs=2πTs\omega_s=\frac{2\pi}{T_s}

根据频域卷积定理

Xp(ω)=F[x(t)p(t)]=12πX(ω)∗P(ω)=1Ts∑n=−∞+∞X(ω−nωs)X_p(\omega)=\mathcal{F}[x(t)p(t)]=\frac{1}{2\pi}X(\omega)*P(\omega)=\frac{1}{T_s}\sum\limits_{n=-\infty}^{+\infty}X(\omega-n\omega_s)

即，采样信号的FTXp(ω)X_p(\omega)为原始信号的X(ω)X(\omega)经过以下步骤得到：

  1. 以ωs\omega_s为周期延拓
  2. 幅度除以TsT_s

回忆，将非周期信号f(t)f(t)以周期为T1T_1周期延拓，频域发生的变化为：

  1. 以ω1\omega_1为周期离散化
  2. 幅度除以T1T_1

二者形成相当完美的对称

Nyquist采样定理

时域采样会使信号在频域发生周期重复，于是，为了使频域周期重复的信号可以恢复出原始信号，原始信号必须满足：

  1. 带限于最高频率ωM\omega_M，即信号的频域分布不超过±ωM\pm\omega_M
  2. ωs>2ωM\omega_s>2\omega_M

讨论

对于采样定理的理解常常有以下误区：

  1. 为什么可以通过采样后的 信息不完整 的信号 完全恢复 出原始信号？
  2. 为什么时域进行 采样 减少信息后，频域发生 周期延拓 反而增加了频谱上的内容？

事实上，我们考虑一个确实带限于采样频率一半的频域信号F(ω)F(\omega)，即：

F(ω)=0, ∀ω:∣ω∣≥ωs2F(\omega)=0,\ \forall\omega:|\omega|\geq\frac{\omega_s}{2}

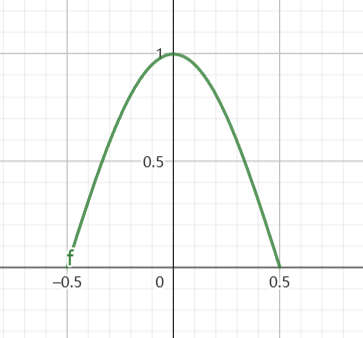
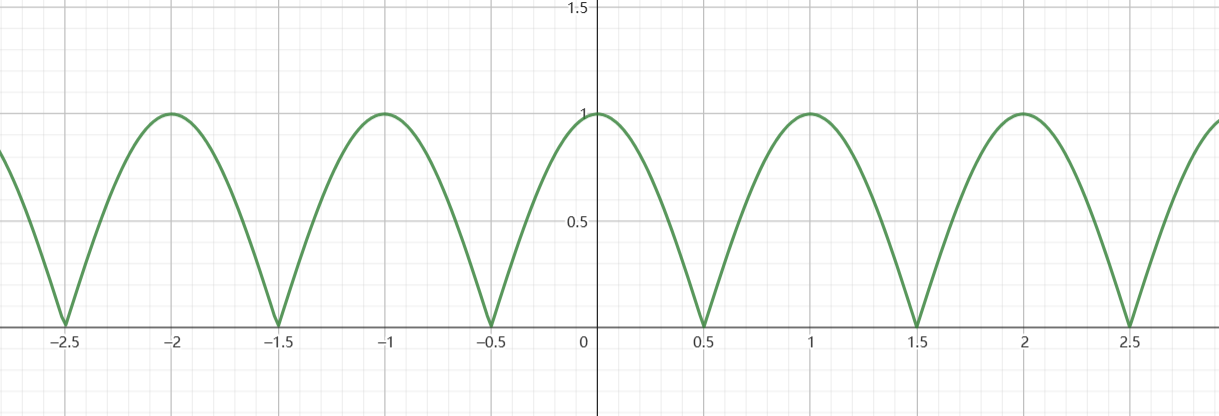
显然，此信号满足Nyquist采样定理的条件，它以ωs\omega_s采样后得到的频谱为

然而，以下两个信号：

F1(ω)=F(ω−ωs)F_1(\omega)=F(\omega-\omega_s)

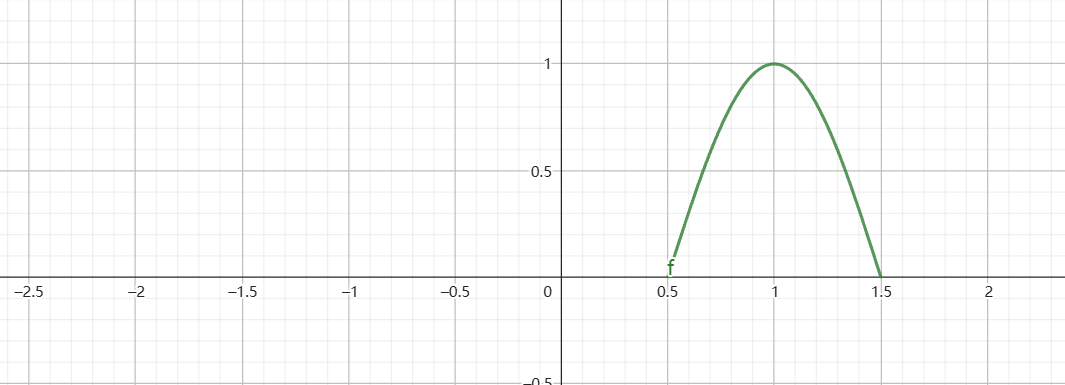
和

F2(ω)=12F(ω)+12F(ω−ωs)F_2(\omega)=\frac{1}{2}F(\omega)+\frac{1}{2}F(\omega-\omega_s)

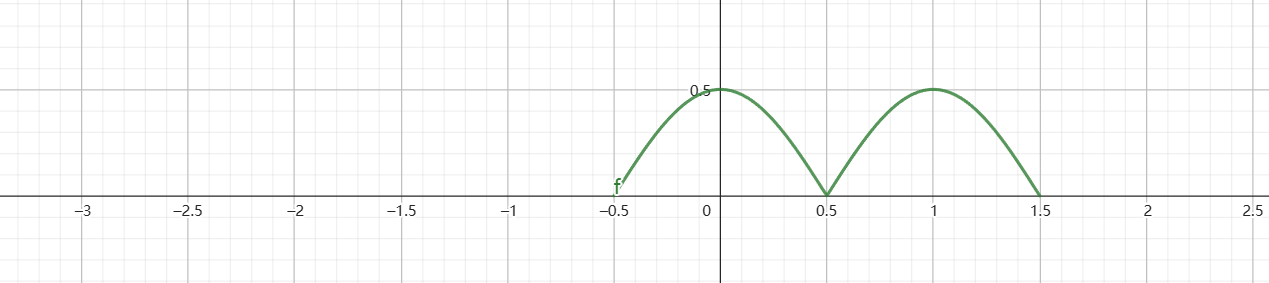
经采样后得到的周期延拓的频谱与F(ω)F(\omega)将会是完全一样的

因此，进行采样导致频谱发生周期延拓这一现象，并不意味着 频域信息增加 ，而是意味着采样后频谱无法分辨差为ωs\omega_s整数倍的频率

这一点从以ωs\omega_s为频率进行采样也可以理解：任何整数倍于ωs\omega_s的倍频信号在此采样下相当于常值

因此，所谓的 满足某些条件的信号可以被唯一恢复 ，实际上只是意味着：

  • 通过周期延拓的频谱可以得到无数个周期延拓前的频谱
  • 但其中只有唯一一个满足带限条件
  • 这无数个频谱在采样点处的值是相同的

内插

上面已经讨论了根据采样信号能够完整恢复原始信号的条件，下面讨论在实际生产中如何进行这个恢复，也就是内插过程

具体来说，内插的做法为在频域乘以一个窗函数（即截取出带限内的频谱），之后进行IFT得到内插后的信号

理想内插

理想内插要求完全恢复符合带限条件的信号本身，故应使用理想低通滤波器的单位冲激响应即h(t)=F−1[Gωs(ω)]h(t)=\mathcal{F}^{-1}[G_{\omega_s}(\omega)]作为内插函数，使用

x(t)=h(t)∗xp(t)x(t)=h(t)*x_p(t)

计算出内插结果

其中

h(t)=12π∫−ωs/2ωs/2ejωtdω=12πjtejωt∣−ωs/2ωs/2h(t)=\frac{1}{2\pi}\int_{-\omega_s/2}^{\omega_s/2}e^{j\omega t}{\rm d}\omega=\frac{1}{2\pi jt}e^{j\omega t}\Bigg|_{-\omega_s/2}^{\omega_s/2}

=2j2πjtsin⁡(ωs2t)=1πtsin⁡(ωs2t)=ωs2πSa(ωs2t)=\frac{2j}{2\pi jt}\sin(\frac{\omega_s}{2}t)=\frac{1}{\pi t}\sin(\frac{\omega_s}{2}t)=\frac{\omega_s}{2\pi}{\rm Sa}(\frac{\omega_s}{2}t)

于是

x(t)=h(t)∗xp(t)=∑n=−∞+∞h(t)∗(xp(nTs)δ(t−nTs))x(t)=h(t)*x_p(t)=\sum\limits_{n=-\infty}^{+\infty}h(t)*(x_p(nT_s)\delta(t-nT_s))

=∑n=−∞+∞xp(nTs)h(t−nTs)=\sum\limits_{n=-\infty}^{+\infty}x_p(nT_s)h(t-nT_s)

即：理想内插本质上是使用若干个Sa{\rm Sa}函数进行平移、拉伸后叠加得到的

然而，理想的低通滤波器（即频域的矩形窗函数）在实际情况中不易得到，往往采取一些近似手段

零阶保持内插

内插函数h0(t)h_0(t)为矩形脉冲函数，故滤波器的通过函数（频域的窗函数）为Sa{\rm Sa}函数

内插结果为每个区间使用其一个端点的采样值代替

一阶保持内插

也叫线性内插，使用三角脉冲函数

h1(t)={tTs+1−Ts<t≤0−tTs+10<t<Tsh_1(t)=\begin{cases} \frac{t}{T_s}+1 & -T_s < t \leq 0 \\ -\frac{t}{T_s}+1 & 0<t<T_s \end{cases}

作为内插函数

可以计算出此时的频域窗函数

H1(ω)=Ts[Sa(ωTs2)]2H_1(\omega)=T_s\big[{\rm Sa}(\frac{\omega T_s}{2})\big]^2