密码学(4) 非对称密码

非对称密码，即公钥密码，基于数学函数而不是代换和置换

六个要素：

• 明文
• 密文
• 公钥
• 私钥
• 加密算法
• 解密算法

符号约定

会话密钥：Ks

用户A的公钥：KUa

用户A的私钥：KRa

用A的公钥对明文P加密：E_KUa[P]

用A的私钥对密文C解密：D_KRa[C]

公钥密码体制

• 公钥公开，用于加密和验证签名
• 私钥保密，用于解密和签名

例：

1. B用公开的KUa对信息加密，密文传递给A，A用KRa解密
2. A用KRa对信息加密（签名），则只有KUa能将其解密，可以验证消息确为A发出

公钥密码的数学原理概述：单向陷门函数

单向陷门函数$f(x)$必须满足以下三个条件：

1. 给定$x$，计算$y=f(x)$是容易的
2. 给定$y$，计算$x$使$y=f(x)$是困难的（即复杂性高到没有实际意义）
3. 存在$\delta$，若知道$\delta$，则计算$x=f^{-1}(y)$是容易的

用途：

1. 加密/解密
2. 数字签名
3. 密钥交换（用于对称密码所需）

分析：

1. 也会受到穷举攻击（安全性不一定高于传统密码）
2. 防范穷举攻击的方法也是使用长密钥
3. 目前主要用于密钥管理和数字签名，加解密仍然使用对称密码（传统密码并未过时，公钥密码进行密钥分配也不比传统密码容易）

数论基础

欧拉函数

$\phi(n)$表示比$n$小且与$n$互素的正整数的个数

设$p,q$是素数，则

1. $\phi(p)=p-1$
2. $\phi(pq)=\phi(p)\phi(q)=(p-1)(q-1)$

欧拉定理

设${\rm gcd}(m,n)=1$，则$m^{\phi(n)}\equiv 1\ {\rm mod}n$

RSA算法

分组密码，明文和密文都是0~n-1之间的整数，n通常是1024位二进制数或309位十进制数

密钥产生：

1. 取两个大素数$p,q$，保密
2. 计算$n=pq$，公开n
3. 计算$\phi(n)=(p-1)(q-1)$
4. 任取与$\phi(n)$互素的小整数$e$
5. 寻找$d$使得$de\equiv 1\ {\rm mod}\phi(n)$，即$de=k\phi(n)+1$
6. 公开$(e,n)$
7. 保密$d$，丢弃$p,q$
8. 公钥为$(e,n)$，私钥为$(d,n)$

加密过程：

1. 将待加密的内容分成k比特的分组，k≤log2n，将每个分组设为$C$
2. 则$E[C]=C^e\ {\rm mod}\ n$

解密过程：

1. $D[C]=C^d\ {\rm mod}\ n$

DH密钥交换算法

本原根与离散对数

对于素数$p$，若$a$满足$1,a,a^2,a^3,...,a^{p-1}$模$p$余数两两不同，则$a$是$p$的一个本原根

本原根指数求模运算的逆运算为离散对数

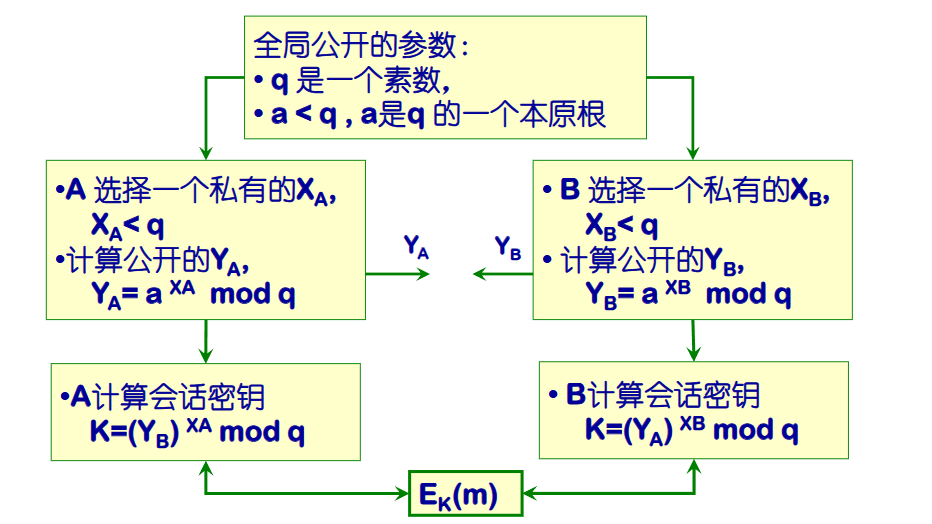
DH密钥交换算法只能用于密钥交换的原因：其目的是计算出一个安全的、两人共享的无意义数字

DSA算法

只能用于数字签名