ALU的实现

不考虑乘除法，ALU整体而言是一个加法器pro max

主要实现思路为根据运算种类来更改超前进位器的计算逻辑，来控制实现的运算

同时需要注意生成一些标志位，如结果为零、结果为负、结果溢出等等

原码乘法及其存储优化

基础算法

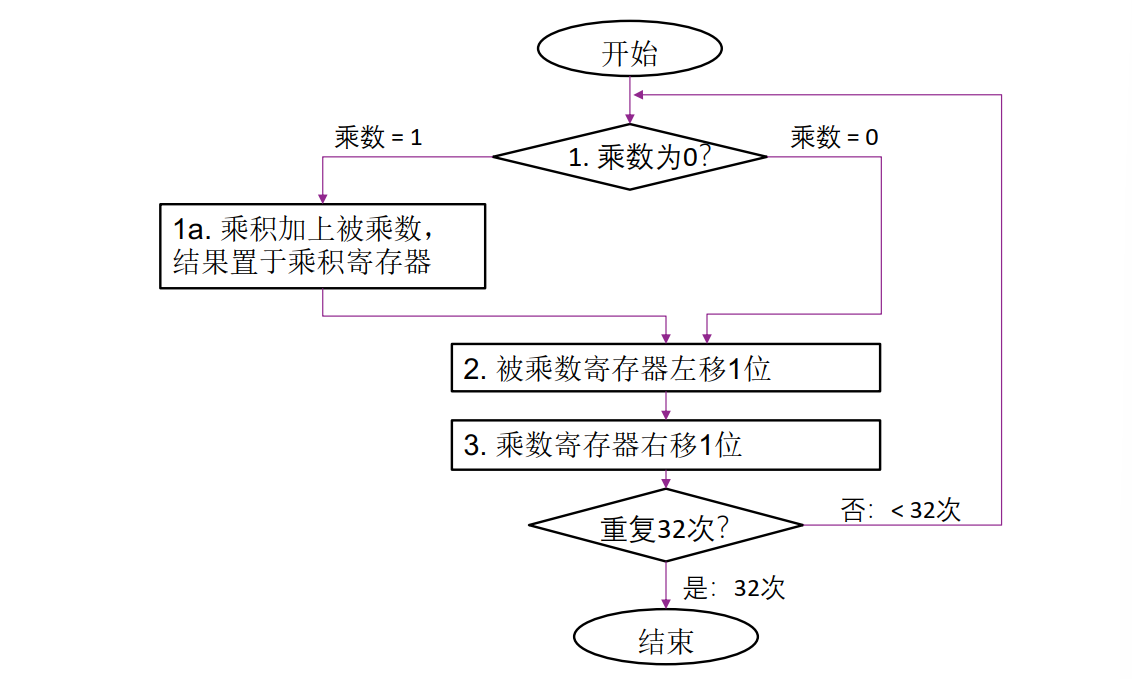
1728185110200

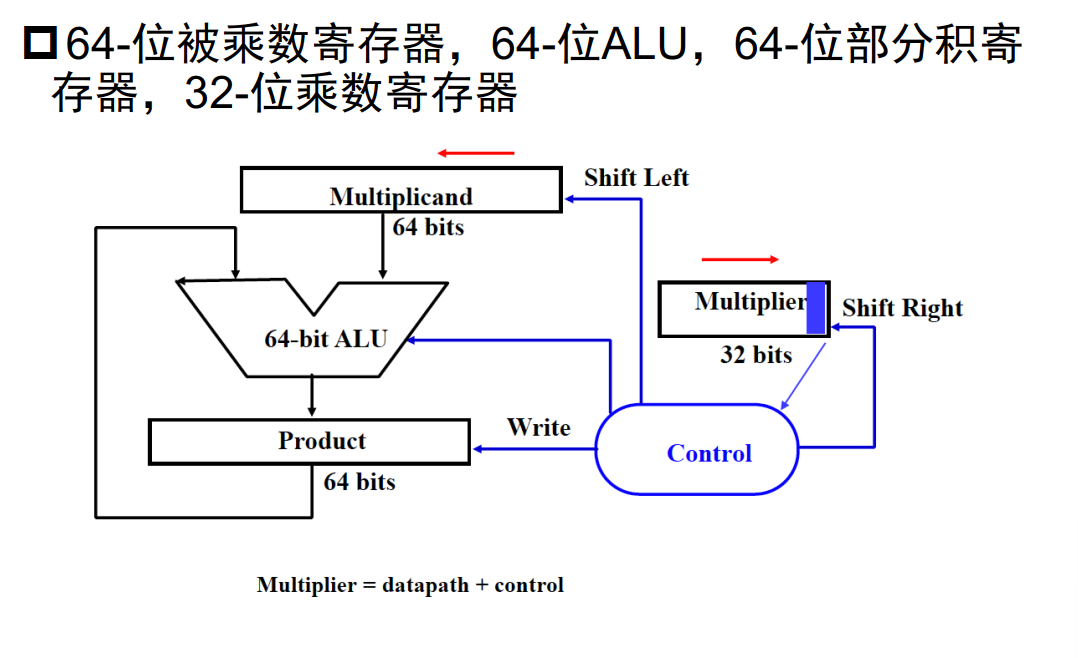
1728185184152

改进1：被乘数没有必要使用64位寄存器，把被乘数的左移改为部分积的右移（计算值永远写入部分积高位）

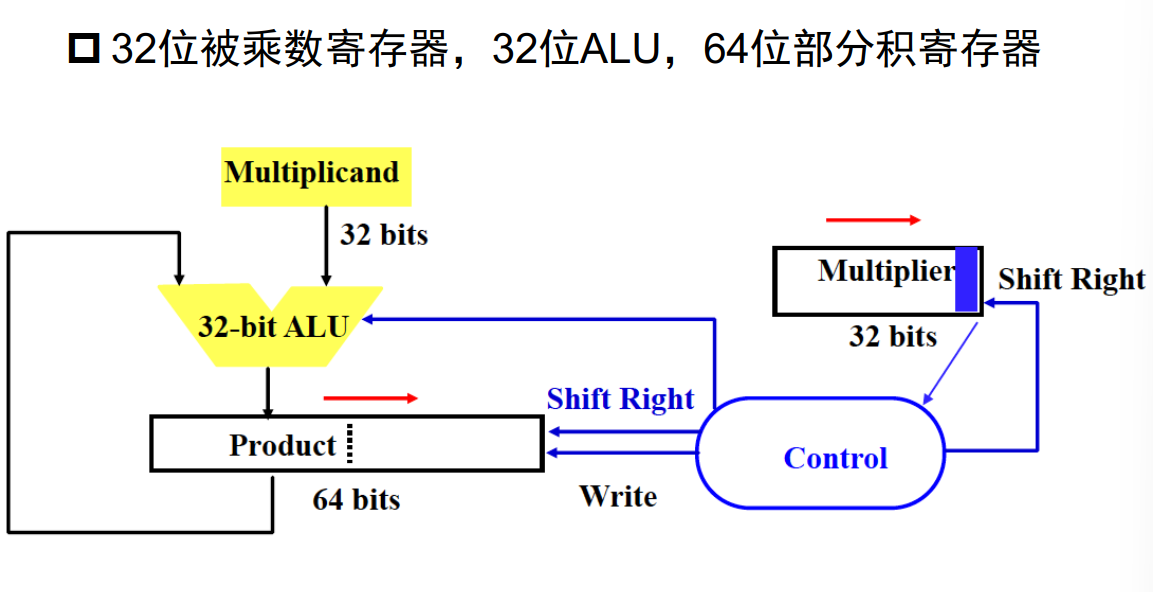
1728185283335

改进2：考虑到部分积位数增长的同时，乘数的位数在减缩；部分积从高位向低位扩展，而乘数在右移；于是可以使用部分积寄存器空置的低位存储乘数

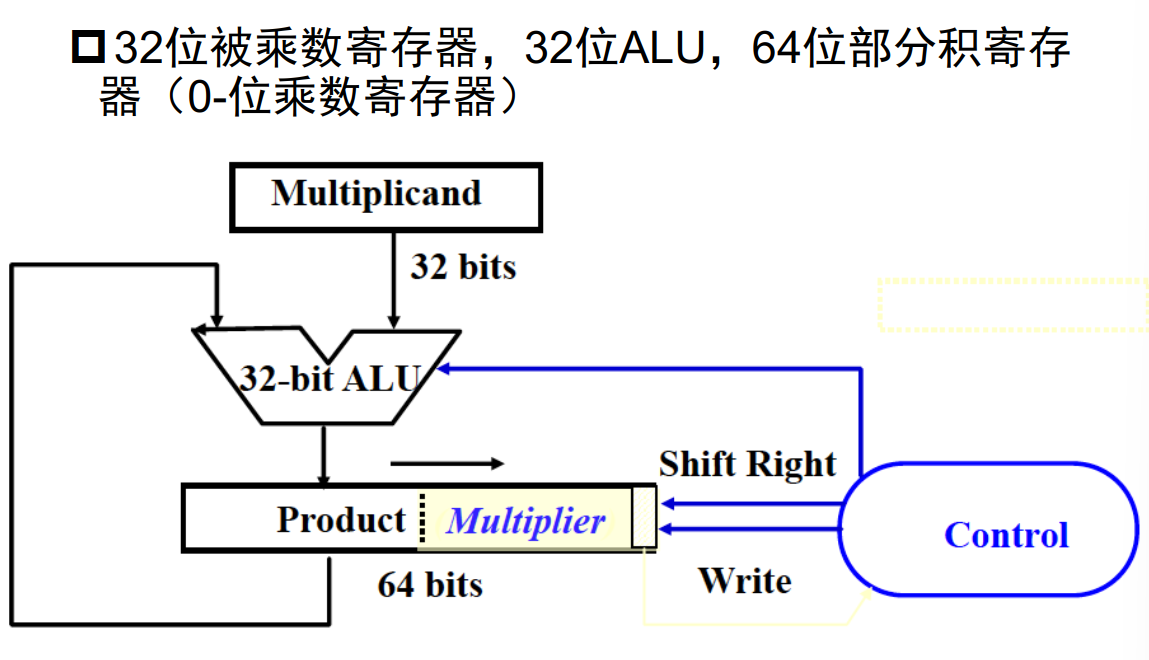
1728185393400

补码乘法：布斯算法

[x×y]c[x\times y]_c =[x]c×y= [x]_c \times y =[x]c×(−2n−1yn−1+∑i=0n−2yi2i)= [x]_c \times (-2^{n-1}y_{n-1} + \sum\limits_{i=0}^{n-2}y_i2^i) =[x]c×[2n−1(yn−2−yn−1)+2n−2(yn−3−yn−2)+...+20(y−1−y0)]= [x]_c \times [2^{n-1}(y_{n-2}-y_{n-1})+2^{n-2}(y_{n-3}-y_{n-2})+...+2^0(y_{-1}-y_0)] =[x]c×∑i=0n−12i(yi−1−yi)= [x]_c \times\sum\limits_{i=0}^{n-1}2^i(y_{i-1}-y_i)

其中y−1=0y_{-1}=0

故：首先对乘数右侧补一位0，之后根据乘数的最低两位取值，若相同则忽略，若01则加被乘数，若10则减被乘数

在计算的过程中，右移为算术右移

在一个部分积寄存器中的实现如下（低位为乘数）

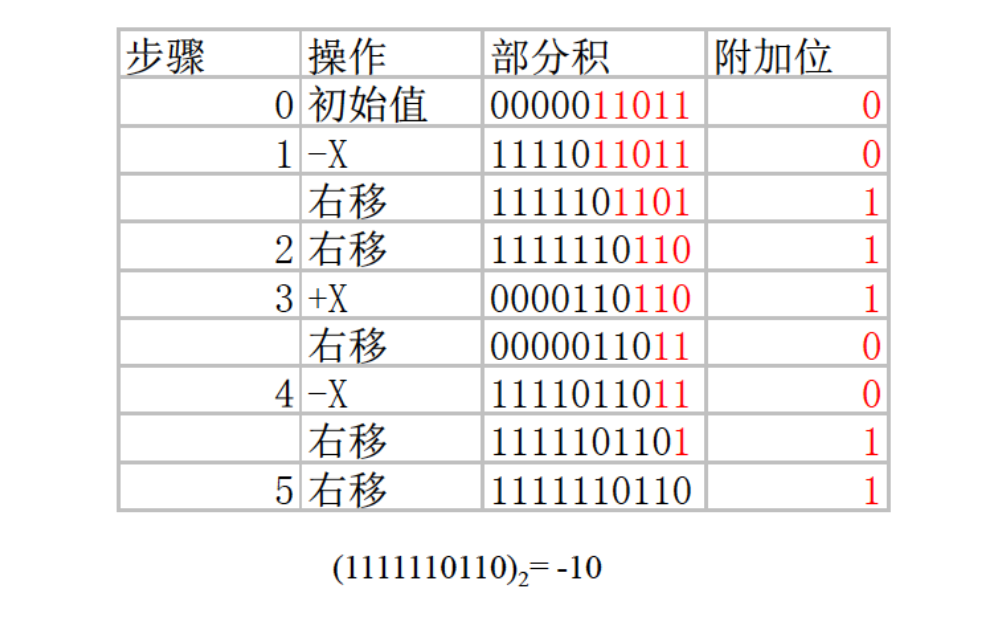
1728186124918

加减交替除法

TODO 还没看:(